- Mateusz Oracz
- 30 maja 2025
Matura z informatyki 2025 już za nami! CKE udostępniła oficjalny arkusz, więc możemy przeanalizować tegoroczne zadania. Sprawdzimy, czy były zgodne z przewidywaniami, na ile przypominały te z poprzednich lat, a także czy pojawiły się nowe, zaskakujące elementy lub potencjalne pułapki.
Zadanie 1: Funkcja Rekurencyjna – Matura z Informatyki 2025

Zadanie 1.1: Analiza Działania Funkcji

Najpierw zobaczmy, jaki jest cel analizy algorytmu. Masz uzupełnić tabelę – wpisać w drugiej kolumnie wynik funkcji przestaw dla podanych wartości argumentu n oraz w trzeciej kolumnie liczbę wywołań funkcji przestaw łącznie z pierwszym wywołaniem z parametrem n.
Jak widzisz, masz podane wartości "n" oraz przykładowe wyniki dla pierwszego "n". Zawsze zaczynaj od analizy algorytmu dla podanego przykładu, żeby sprawdzić, czy dobrze rozumiesz schemat działania. Weźmy przykładowe n = 316 498 i wróćmy do pseudokodu. Przy rozwiązywaniu takiego zadania na maturze dobrym pomysłem będzie także przepisanie algorytmu na kod i uruchomienie go w celu sprawdzenia obliczeń.
Algorytm w każdym wywołaniu:
- r – wyciąga dwie ostatnie cyfry liczby (lub jedną, gdy liczba jest jednocyfrowa)
- a – pierwsza cyfra z r (r div 10)
- b – druga cyfra z r (r mod 10)
- n – zmniejsza się o wyciągnięte cyfry (n div 100)
Pierwsze wywołanie:
W pierwszym wywołaniu wywołujemy funkcję przestaw z argumentem 316498.

Drugie wywołanie:
Następnie wywołujemy przestaw(3164).
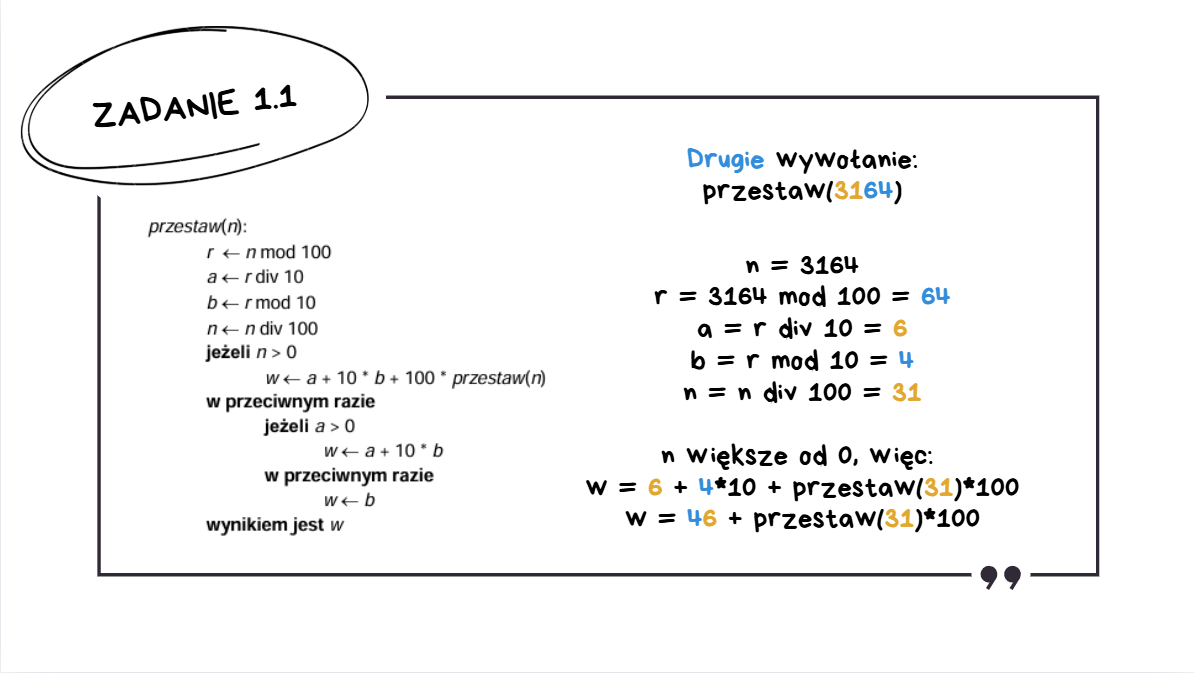
Trzecie wywołanie:
Trzecie wywołanie jest tym ostatnim.
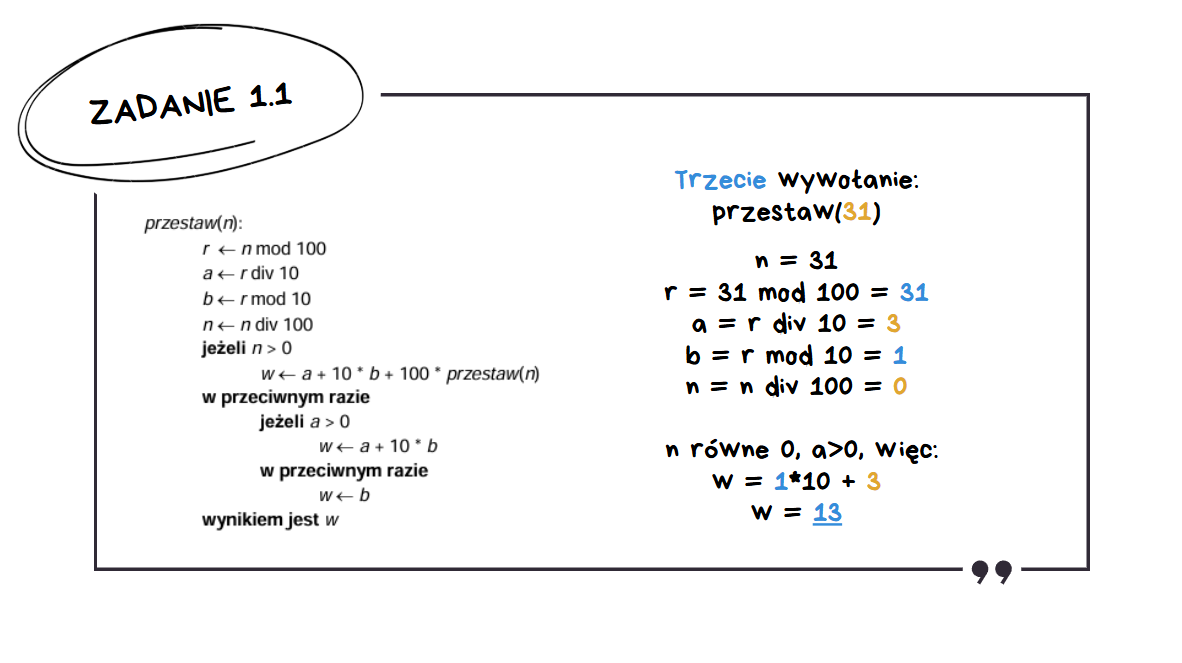
Powrót z rekurencji:
- przestaw(31) = 13
- przestaw(3164) = 6 + 40 + 13×100 = 1346
- przestaw(316498) = 9 + 80 + 1346×100 = 134689
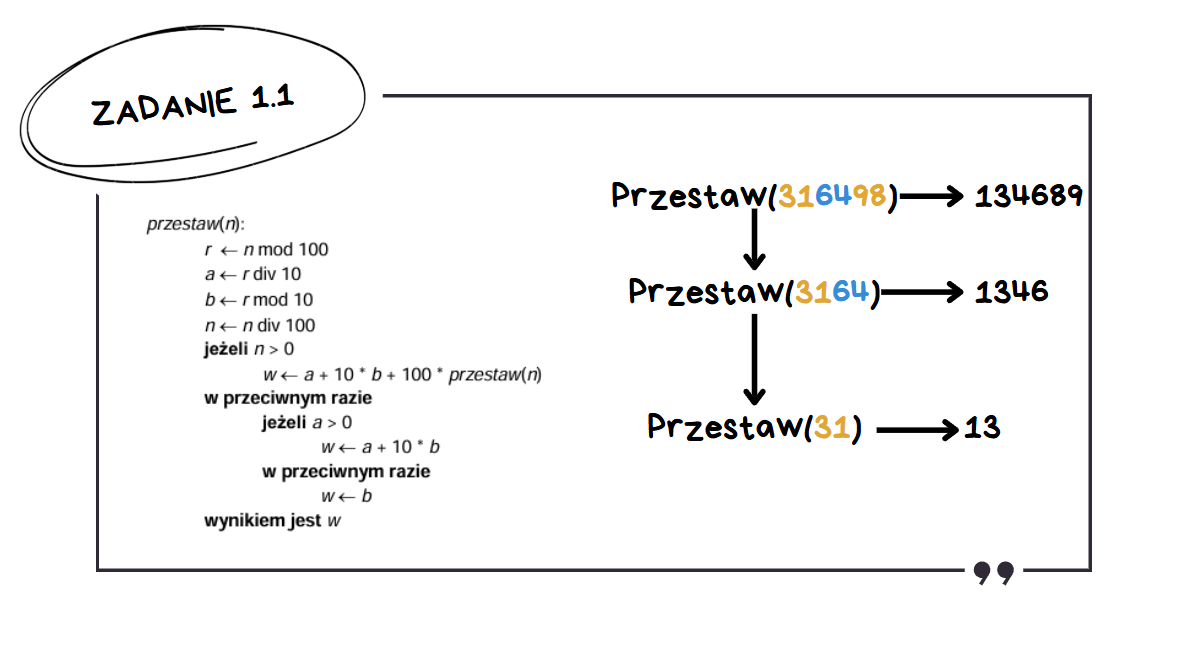
Wynik: 134689
Liczba wywołań: 3
Schemat jest prosty: pobieramy dwie ostatnie cyfry i zamieniamy je miejscami.
Zadanie 1.1 matura informatyka 2025 odpowiedź:

Zadanie 1.2: Prawda/Fałsz
Zadanie sprawdzało umiejętność określenia liczby wywołań funkcji rekurencyjnej w zależności od liczby cyfr k.

Przy ocenie prawdziwości danego wzoru należało wziąć pod uwagę dwa przypadki – k jest nieparzyste oraz k jest parzyste.
1) Liczba wywołań = k/2 – FAŁSZ
- Dla parzystego k = 8: 8/2 = 4 ✓
- Dla nieparzystego k = 9: 9/2 = 4,5 – nie można mieć połowy wywołania
2) Liczba wywołań = (k+1) div 2 – PRAWDA
- Dla parzystego k = 8: (8+1) div 2 = 4 ✓
- Dla nieparzystego k = 9: (9+1) div 2 = 5 ✓
3) Liczba wywołań = k/2 dla parzystych, (k+1)/2 dla nieparzystych – PRAWDA
- Dla parzystego k = 8: 8/2 = 4 ✓
- Dla nieparzystego k = 9: (9+1)/2 = 5 ✓
4) Liczba wywołań = (k+1)/2 – FAŁSZ
- Dla parzystego k = 8: (8+1)/2 = 4,5 – wyniki nie mogą być niecałkowite
- Dla nieparzystego k = 9: (9+1)/2 = 5 ✓
Zadanie 1.2 matura informatyka 2025 odpowiedź:
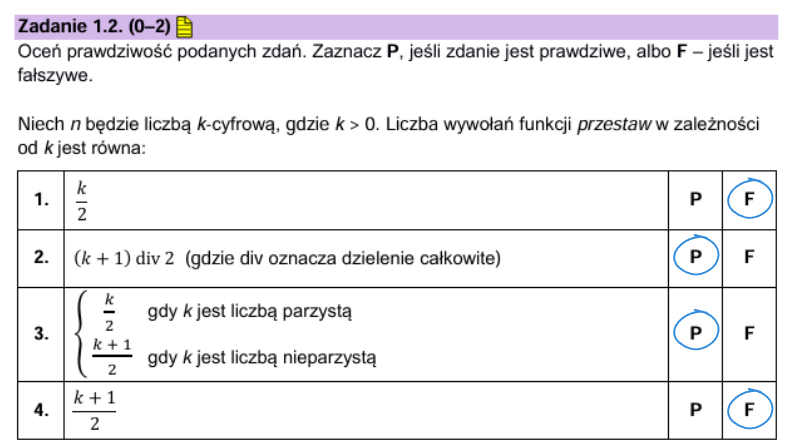
Zadanie 1.3: Implementacja Iteracyjna

Ostatni podpunkt wymagał przepisania funkcji rekurencyjnej na wersję iteracyjną. Należy zwrócić szczególną uwagę na dopisek "Uwaga". Wynika z niego wprost, że w tym algorytmie musisz działać wyłącznie na liczbach całkowitych – nie możesz np. zamienić liczby na tekst czy tablicę – skutkowałoby to nieuznaniem rozwiązania.
W jaki sposób zamienić funkcję rekurencyjną na iteracyjną?
- Zamiast rekurencji używamy pętli.
- Odczytujemy liczby parami.
- Wykorzystujemy pomocniczą zmienną mnożnik, przez którą będziemy mnożyć aktualną parę przed dodaniem jej do wyniku – w celu ustawienia jej na właściwej pozycji.
- W każdej iteracji zwiększamy mnożnik razy 100.
def przestaw2(n):
if n == 0:
return 0
x = 0
w = 0
mnoznik = 1
while n > 0:
r = n % 100
a = r // 10
b = r % 10
n = n // 100
if a > 0 or n > 0:
x = a + 10 * b
else:
x = b
# Dodajemy do wyniku z odpowiednim mnożnikiem
w += x * mnoznik
# Zwiększamy mnożnik dla następnej pary cyfr
mnoznik *= 100
return wTo banalne zadanie – podstawa matury z informatyki, czyli sprawna zamiana między iteracją a rekurencją. Z komputerem pod ręką na maturze to już w ogóle banał!
Zadanie 2: Zapis Symboliczny – Matura z Informatyki 2025

Zadanie 2. dotyczyło analizy pliku symbole.txt zawierającego 2000 napisów. Każdy napis składał się z dokładnie 12 znaków spośród: `o`, `+`, `*`. Jest to typowe zadanie programistyczne – w poleceniu jest wprost napisane, że należy napisać program.
Zadanie 2.1: Palindromy

Bardzo proste zadanie – należało znaleźć wszystkie napisy będące palindromami (czytane od przodu i od tyłu są identyczne). W naszym kursie temat palindromów poruszany był tyle razy, że jest to już trochę mem naszego przygotowania.
W kodzie wczytujemy linie pojedynczo z pliku. Każda linia jest reprezentowana jako napis. Tworzymy funkcję pomocniczą o nazwie czy_palindrom, w której implementujemy pętlę porównującą znaki napisu. Pętla przerywa swoje działanie w momencie znalezienia pierwszej różnicy między odpowiadającymi sobie elementami. Inną, prostszą opcją byłoby skorzystanie z funkcji wbudowanej do obracania napisów – wystarczyłoby wtedy obrócić napis i sprawdzić czy odwrócony wygląda dokładnie tak samo jak pierwotny.
def czy_palindrom(napis):
dlugosc = len(napis)
for i in range(dlugosc // 2):
if napis[i] != napis[dlugosc - 1 - i]:
return False
return True
plik_wyjsciowy = open('wyniki2.txt', 'w')
plik_wyjsciowy.write("2.1.\n")
plik_wejsciowy = open('symbole.txt', 'r')
for linia in plik_wejsciowy:
napis = linia.strip()
if czy_palindrom(napis):
plik_wyjsciowy.write(napis + "\n")
plik_wejsciowy.close()
plik_wyjsciowy.close()
Odpowiedzią w tym zadaniu było sześć napisów:
++o+o++o+o++
+*+**++**+*+
*+o++**++o+*
*oo*o**o*oo*
+*++*oo*++*+
+o++oooo++o+
Zadanie na poziomie starych matur na poziomie podstawowym, idealne na rozgrzewkę.
Zadanie 2.2: Analiza Sąsiadów

Kolejne zadanie przypomina, legendarne już zadanie z matury 2016 – "grę w życie", które realizowaliśmy podczas przygotowania. Było to stosunkowo trudne zadanie, jednak na szczęście tutaj tylko forma jest podobna – poziom trudności i złożoność już nie. Tam też musieliśmy sprawdzać sąsiadów komórki. Ale tam było trudniej, bo albo komórka umierała, albo się regenerowała w zależności od liczby żyjących sąsiadów. I były jeszcze kolejne pokolenia. Tutaj nie musimy przeprowadzać żadnej symulacji – wystarczy jedynie sprawdzić dla każdej komórki jej sąsiadów.
- Zaczynamy od wczytania znaków z pliku do tablicy stringów i w ten sposób tworzymy macierz.
- Przechodzimy po każdym znaku macierzy, pomijając te skrajne (pierwszy i ostatni wiersz oraz pierwszą i ostatnią kolumnę – tam na pewno nie ma wszystkich potrzebnych sąsiadów).
- Wywołujemy funkcję czy_kwadrat która sprawdza, czy znak i sąsiedzi są takie same: za pomocą dwóch pętli przechodzących po wszystkich sąsiadach – jeśli znajdzie błąd, zwróci fałsz, jeśli przejdzie bezbłędnie, zwróci prawdę.
- W głównej części programu, gdy funkcja czy_kwadrat zwróci prawdę – należy zwiększyć liczbę przechowującą liczbę wystąpień takiej sytuacji oraz zapisać numery wiersza i kolumny w tablicy.
def czy_kwadrat(macierz, wiersz, kolumna):
znak_centralny = macierz[wiersz][kolumna]
for i in range(wiersz-1, wiersz+2):
for j in range(kolumna-1, kolumna+2):
if macierz[i][j] != znak_centralny:
return False
return True
plik = open('symbole.txt', 'r')
macierz = []
for linia in plik:
macierz.append(linia.strip())
plik.close()
plik = open('wyniki2.txt', 'a')
plik.write("2.2.\n")
licznik_kwadratow = 0
kwadraty = []
for wiersz in range(1, len(macierz)-1):
for kolumna in range(1, len(macierz[wiersz])-1):
if czy_kwadrat(macierz, wiersz, kolumna):
licznik_kwadratow += 1
kwadraty.append([wiersz+1, kolumna+1])
plik.write(str(licznik_kwadratow) + "\n")
for kwadrat in kwadraty:
wiersz = kwadrat[0]
kolumna = kwadrat[1]
plik.write(f"{wiersz} {kolumna}\n")
plik.close()Banalne zadanie wymagające jedynie umiejętności operowania na macierzach.
Odpowiedź:
3
399 5
546 2
630 11
Zadanie 2.3: Konwersja z Systemu Trójkowego

Bardzo przyjemne zadanie, podczas wczytywania znaków zamieniamy znaki na cyfry i od razu pakujemy je do stringa, ponieważ mamy system trójkowy i będziemy robić jego konwersję na dziesiętny.
Warto też tutaj przypomnieć, to co zawsze mówię, nie ma co się uczyć jak działają konkretne systemy liczbowe, tylko najlepiej nauczyć się ogólnej logiki za nimi stojącej – w takim wypadku nie ma znaczenia czy na maturze pojawi się system dwójkowy, trójkowy czy może siódemkowy.
Systemy liczbowe, tyle razy pojawiały się na maturach, że każdy idący na maturę z informatyki powinien autentycznie cieszyć się z takiego zadania.
- Robimy funkcję zamieniającą z trójkowego na dziesiętny.
- Jeśli wczytana liczba jest większa od maksymalnej, to zapisujemy nową maksymalną – zarówno w systemie trójkowym, jak i dziesiętnym.
- Na końcu zapisujemy wyniki do pliku tekstowego.
def zamien_na_dziesietny(napis):
trojkowy = ""
for znak in napis:
if znak == 'o':
trojkowy += '0'
elif znak == '+':
trojkowy += '1'
elif znak == '*':
trojkowy += '2'
dziesietny = 0
potega = 1
for cyfra in reversed(trojkowy):
dziesietny += int(cyfra) * potega
potega *= 3
return dziesietny
plik_wejsciowy = open('symbole.txt', 'r')
max_liczba = 0
max_napis = ""
for napis in plik_wejsciowy:
napis = napis.strip()
liczba = zamien_na_dziesietny(napis)
if liczba > max_liczba:
max_liczba = liczba
max_napis = napis
plik_wyjsciowy = open('wyniki2.txt', 'a')
plik_wyjsciowy.write(f"2.3. \n{max_liczba} {max_napis}\n")
plik_wyjsciowy.close()
plik_wejsciowy.close() Odpowiedź:
Liczba w dziesiętnym: 531246
Liczba symbolicznie: *******o+*+o
Zadanie 2.4: Sumowanie

Tutaj możemy skorzystać z kodu z poprzedniego zadania, zamieniającego liczby z trójkowego na dziesiętny do obliczenia sumy, a następnie wystarczy dodać funkcję zamieniającą sumę na symbole trójkowe.
def zamien_na_dziesietny(napis):
trojkowy = ""
for znak in napis:
if znak == 'o':
trojkowy += '0'
elif znak == '+':
trojkowy += '1'
elif znak == '*':
trojkowy += '2'
dziesietny = 0
potega = 1
for cyfra in reversed(trojkowy):
dziesietny += int(cyfra) * potega
potega *= 3
return dziesietny
def zamien_na_trojkowe_symbole(liczba):
if liczba == 0:
return "o"
trojkowe_symbole = ""
while liczba > 0:
reszta = liczba % 3
if reszta == 0:
trojkowe_symbole = "o" + trojkowe_symbole
elif reszta == 1:
trojkowe_symbole = "+" + trojkowe_symbole
else:
trojkowe_symbole = "*" + trojkowe_symbole
liczba //= 3
return trojkowe_symbole
plik_wejsciowy = open('symbole.txt', 'r')
suma = 0
for napis in plik_wejsciowy:
liczba = zamien_na_dziesietny(napis.strip())
suma += liczba
suma_trojkowa = zamien_na_trojkowe_symbole(suma)
plik_wyjsciowy = open('wyniki2.txt', 'a')
plik_wyjsciowy.write(f"2.4.\n {suma} {suma_trojkowa}\n")
plik_wyjsciowy.close() Odpowiedź:
Suma wszystkich liczb: 527865439
W zapisie trójkowym: ++oo*+oo*++ooo*o*++
Zgodnie z poleceniem – wyniki powinny zostać zapisane w pliku wyniki2.txt. Bez zapisania wyników w pliku .txt nie dostaniesz punktów za zadanie, nawet jeżeli rozwiązałeś je poprawnie. Przykładowo wypełniony plik .txt został przedstawiony poniżej.

Podsumowując: zadanie 2. było naprawdę przyjemne i proste. Wymagało tylko podstawowej wiedzy o:
- Palindromach
- Pracy z macierzami
- Systemach liczbowych
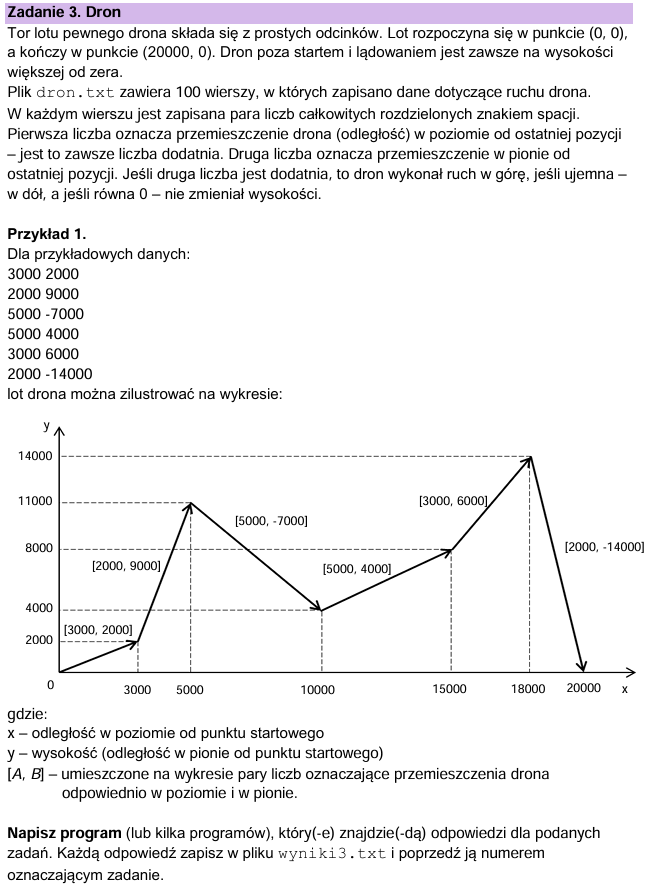
Zadanie 3: Dron – Matura z Informatyki 2025
Zadanie 3. jest zadaniem z bardzo długim poleceniem, ale rozwiązania poszczególnych podpunktów nie były szczególnie skomplikowane.
Zadanie 3.1: Największy Wspólny Dzielnik (NWD)

To zaskakujące, że NWD pojawił się na maturze – jest to jeden z najbardziej podstawowych algorytmów. Algorytm Euklidesa jest jednym z pierwszych poruszanych u nas w kursie w module dotyczącym algorytmów. Jeżeli jednak jesteś osobą, która przygotowuje się do matury z informatyki – specjalnie dla Ciebie krótkie omówienie algorytmu Euklidesa.
Jak działa algorytm Euklidesa?
Algorytm Euklidesa umożliwia efektywne obliczenie największego wspólnego dzielnika dwóch liczb (największej liczby całkowitej, która dzieli wartości A i B bez reszty). Polega on na wykonywaniu operacji modulo do momentu, aż reszta z dzielenia będzie równa 0.

def nwd(a, b):
a = abs(a)
b = abs(b)
if a == 0:
return b
if b == 0:
return a
while b != 0:
reszta = a % b
a = b
b = reszta
return a
plik_wejsciowy = open('dron.txt', 'r')
pary_z_nwd_wiekszym_od_1 = 0
for linia in plik_wejsciowy:
liczby = linia.strip().split()
a = int(liczby[0])
b = int(liczby[1])
nwd_ab = nwd(a, b)
if nwd_ab > 1:
pary_z_nwd_wiekszym_od_1 += 1
plik_wejsciowy.close()
plik_wyjsciowy = open('wyniki3.txt', 'w')
plik_wyjsciowy.write(f"3.1. \n{pary_z_nwd_wiekszym_od_1}\n")
plik_wyjsciowy.close() Odpowiedź:
Liczba par z NWD większym od 1: 40
Zadanie 3.2a: Dron w Kwadracie

- Bierzemy poszczególne punkty z pliku tekstowego.
- Obliczamy aktualny stan drona.
- Jeśli jest w zakresie kwadratu, dodajemy do licznika.
- Na końcu zapisujemy licznik do pliku.
def czy_wewnatrz_kwadratu(x, y):
return 0 < x < 5000 and 0 < y < 5000
plik_wejsciowy = open('dron.txt', 'r')
pozycja_x = 0
pozycja_y = 0
punkty_wewnatrz = 0
for linia in plik_wejsciowy:
liczby = linia.strip().split()
dx = int(liczby[0])
dy = int(liczby[1])
pozycja_x += dx
pozycja_y += dy
if czy_wewnatrz_kwadratu(pozycja_x, pozycja_y):
punkty_wewnatrz += 1
plik_wejsciowy.close()
plik_wyjsciowy = open('wyniki3.txt', 'a')
plik_wyjsciowy.write(f"3.2. a)\n{punkty_wewnatrz}\n")
plik_wyjsciowy.close()Proste zadanie wymagające tylko dodawania i odejmowania współrzędnych.
Odpowiedź:
Liczba punktów wewnątrz kwadratu: 24
Zadanie 3.2b: Środki Odcinków
To najbardziej złożony podpunkt zadania 3. Algorytm wymaga sprawdzenia wszystkich możliwych par punktów i obliczenia środka każdego odcinka.
Co możesz zrobić? Dla każdej możliwej pary punktów obliczyć środek odcinka i sprawdzić, czy jest on również w danych.
Jak wyznaczyć środek odcinka?
Środek odcinka wyznaczymy licząc średnią ze współrzędnych X i współrzędnych Y. W ten sposób otrzymamy współrzędne (X, Y) środka.
- Robimy dwie pętle – jedna określa pierwszy punkt, druga drugi punkt.
- Pomijamy, jeśli oba punkty są takie same (aby uniknąć błędów).
- Określamy środek punktów: środek_x = (x1 + x2) / 2 , środek_y = (y1 + y2) / 2.
- Sprawdzamy, czy środek również jest w tablicy z danymi.
- Jeśli znajdziemy – kończymy działanie algorytmu.
plik = open('dron.txt', 'r')
dane = []
for linia in plik:
liczby = linia.strip().split()
dx = int(liczby[0])
dy = int(liczby[1])
dane.append((dx, dy))
plik.close()
wszystkie_punkty = []
pozycja_x = 0
pozycja_y = 0
wszystkie_punkty.append((pozycja_x, pozycja_y))
for i in range(len(dane)):
dx = dane[i][0]
dy = dane[i][1]
pozycja_x = pozycja_x + dx
pozycja_y = pozycja_y + dy
wszystkie_punkty.append((pozycja_x, pozycja_y))
znaleziona_trojka = None
for i in range(len(wszystkie_punkty)):
for j in range(len(wszystkie_punkty)):
if i == j:
continue
punkt1 = wszystkie_punkty[i]
punkt3 = wszystkie_punkty[j]
srodek_x = (punkt1[0] + punkt3[0]) / 2
srodek_y = (punkt1[1] + punkt3[1]) / 2
srodek = (srodek_x, srodek_y)
if srodek in wszystkie_punkty:
znaleziona_trojka = (punkt1, srodek, punkt3)
break
if znaleziona_trojka:
break
plik = open('wyniki3.txt', 'a')
punkt1 = znaleziona_trojka[0]
punkt2 = znaleziona_trojka[1]
punkt3 = znaleziona_trojka[2]
plik.write(f"3.2. b)\n({punkt1[0]}, {punkt1[1]}), ({punkt2[0]}, {punkt2[1]}), ({punkt3[0]}, {punkt3[1]})\n")
plik.close()Bardziej złożone niż poprzednie podpunkty, ale nadal proste. Wymaga dwukrotnego przeszukania listy oraz sprawdzenia obecności środka.
Odpowiedź:
Znaleziona trójka punktów:
(5832, 1801),
(7410, 1990),
(8988, 2179)
Analogicznie jak w poprzednim zadaniu należy zapisać wyniki w pliku .txt.

Zadanie 4: Czym jest Keylogger? – Matura z Informatyki 2025

Zadanie wymagające po prostu znajomości definicji – nawet można było się domyśleć odpowiedzi. Jako key w informatyce często określa klawisze klawiatury np. Enter key, Return key. Log jak logować, czyli zapisywać informacje. Odpowiedź poprawna to odpowiedź D.
Jeśli chcesz mieć pewność, że poradzisz sobie z pytaniami teoretycznymi na maturze, sięgnij po książkę Matura Informatyka Teoria. Dzięki niej oraz dołączonym materiałom wideo zyskasz solidną bazę wiedzy i odpowiedzi na wszystkie typowe pytania teoretyczne.
W ramach dodatkowego wsparcia w procesie nauki, przygotowaliśmy dla Ciebie książkę „MATURA INFORMATYKA - TEORIA”.
Materiały zostały stworzone z myślą o zróżnicowanych stylach nauki – zarówno w formie czytanej, jak i słuchanej – aby ułatwić przyswajanie wiedzy i zwiększyć efektywność Twojej nauki.

Zadanie 5: Dodawanie w systemie binarnym – Matura z Informatyki 2025
To zadanie stanowiło pewną nowość – dodawanie pisemne liczb binarnych z lukami jeszcze się nie pojawiało na maturach, choć systemy liczbowe to klasyka. Pokazuje to, jak ważne jest opanowanie operacji arytmetycznych we wszystkich systemach, a nie tylko umiejętność konwersji na system dziesiętny.
Jak dodawać pisemnie w Systemie Binarnym?
Pisemne dodawanie liczb binarnych jest analogiczne do pisemnego dodawania liczb dziesiętnych, które znasz ze szkoły. Jeżeli suma liczb w kolumnie będzie większa lub równa podstawie systemu (czyli 2), to następuje przeniesienie tego nadmiaru do kolejnej kolumny.
Podstawowe reguły:
- 0 + 0 = 0
- 0 + 1 = 1
- 1 + 0 = 1
- 1 + 1 = 0 (i 1 do przeniesienia)
- 1 + 1 + 1 = 1 (i 1 do przeniesienia)
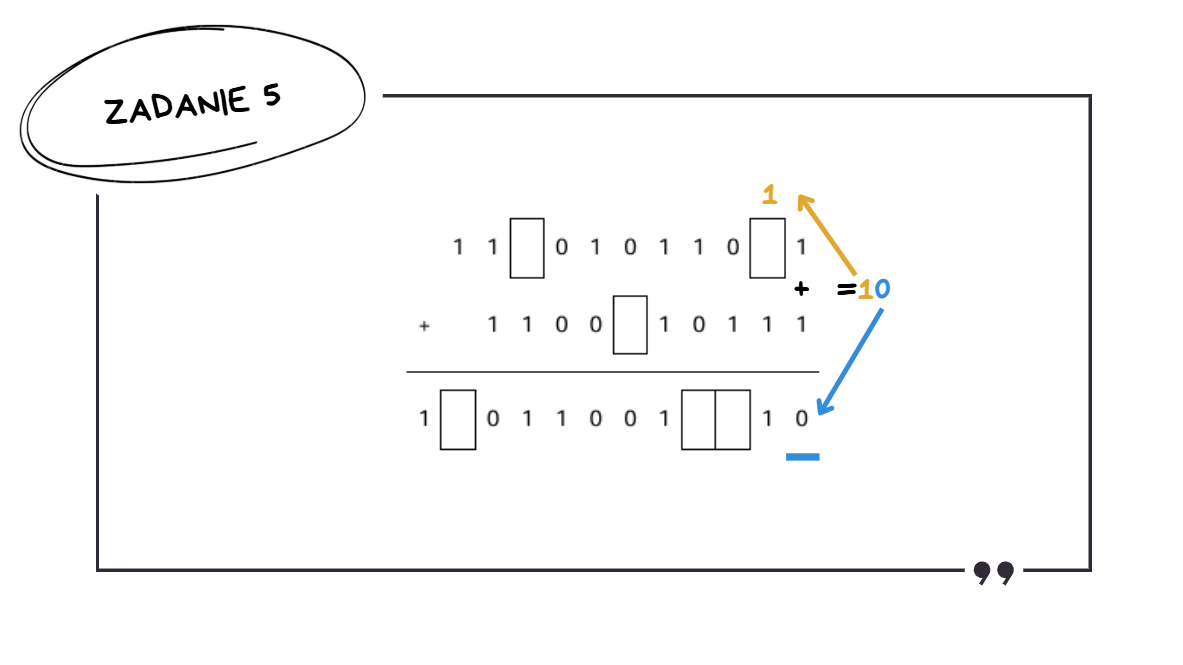
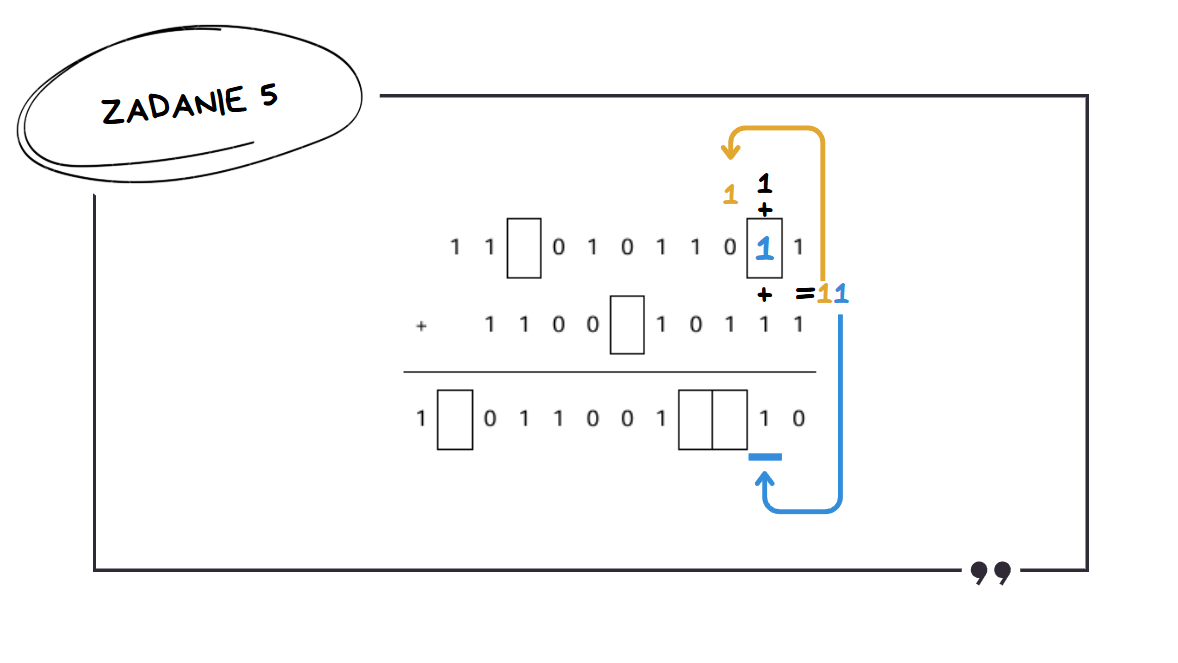
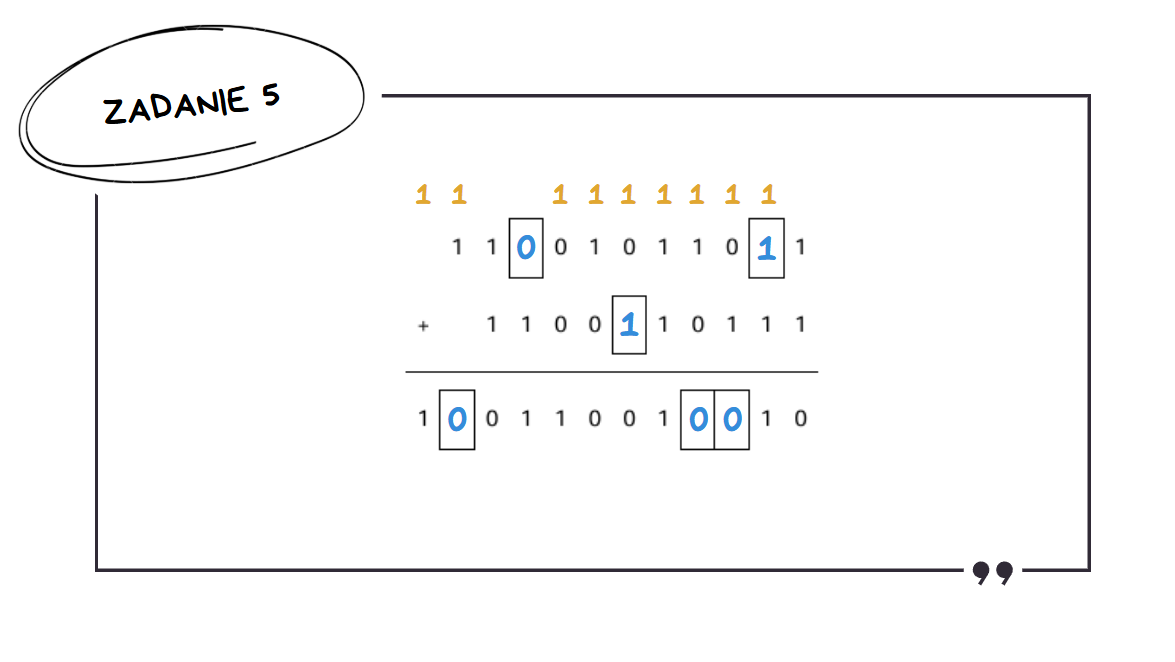
I tak dalej, wypełniając kolejne puste pola zgodnie z logiką dodawania binarnego.
Zadanie 6: Martianeum – Matura z Informatyki 2025

Zadanie 6.1: Obliczanie Łącznej Masy

Pułapki w zadaniu:
- Wartości procentowe: zawartość podana w %, a nie jako ułamek dziesiętny.
- Próg wydobycia: tylko ładunki z zawartością ≥ 1% są wydobywane.
Po wczytaniu danych z pliku .txt należy, obliczamy na początku łączną masę ładunków – korzystając z funkcji suma odwołującej się do kolumny masa.
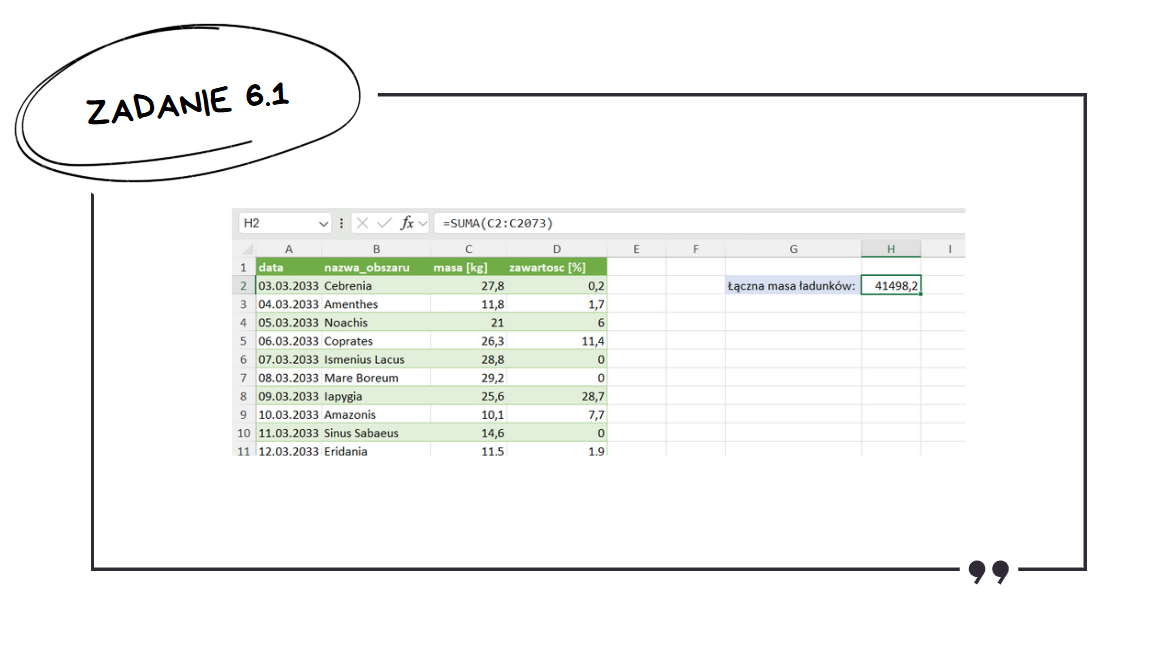
Następnie należy dodać kolumnę, w której obliczone zostanie wydobyte martianeum – jeżeli zawartość martianeum wynosi co najmniej 1% to mnożymy masę ładunku razy zawartość, w przeciwnym wypadku nic nie zostało wydobyte. Zawartość dzielimy przez sto, aby przekonwertować ją z procentów na ułamek dziesiętny.
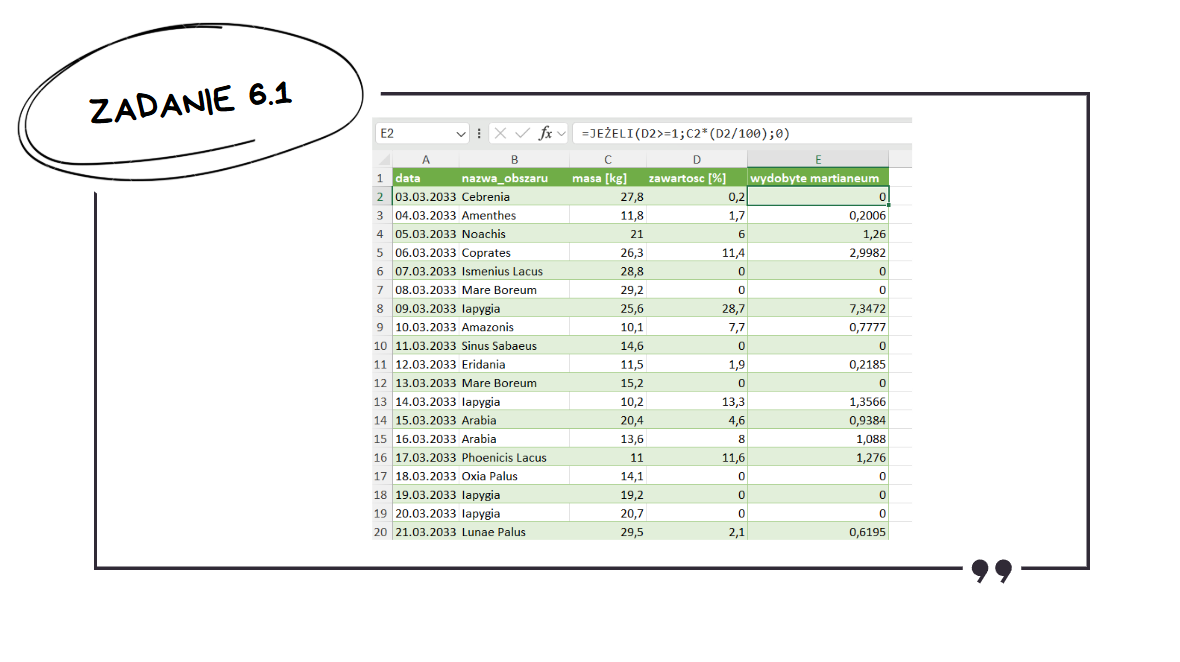
Na końcu należy zsumować wartości w kolumnie z wydobytym martianeum.
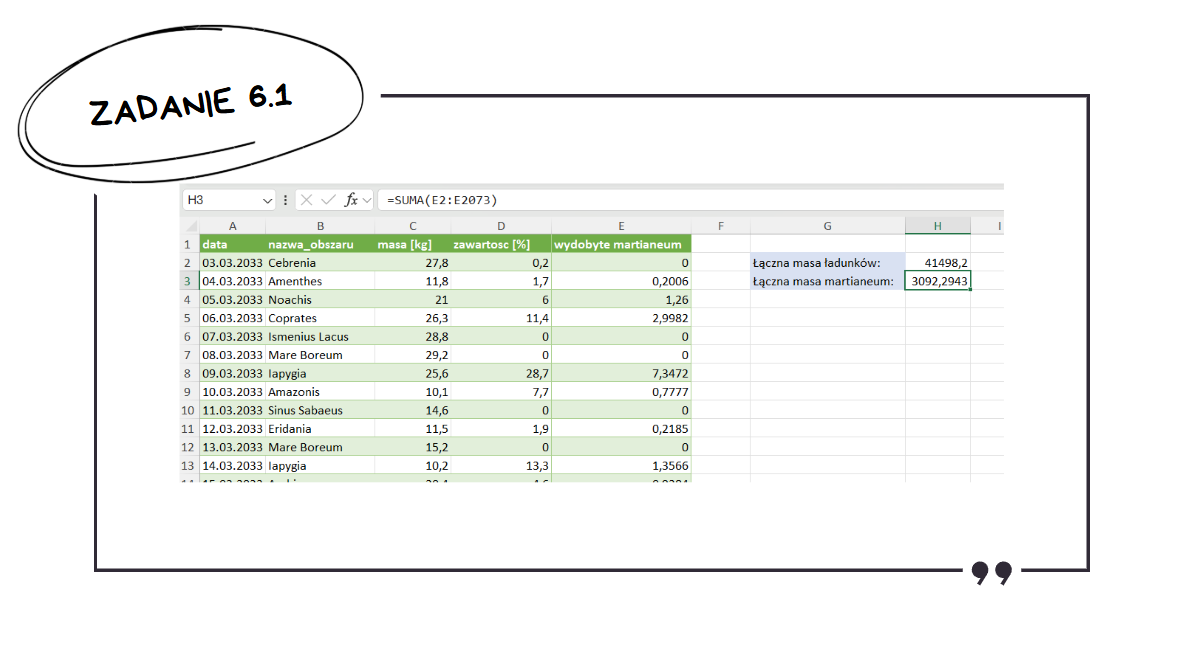
Zadanie 6.2: Średnia Masa wg Obszarów

To zadanie jest idealnym zadaniem do wykonania za pomocą tabeli przestawnej. Po utworzeniu tabeli przestawnej, w której policzona zostanie średnia masa, należy tylko posortować tę tabelę od najmniejszych do największych.
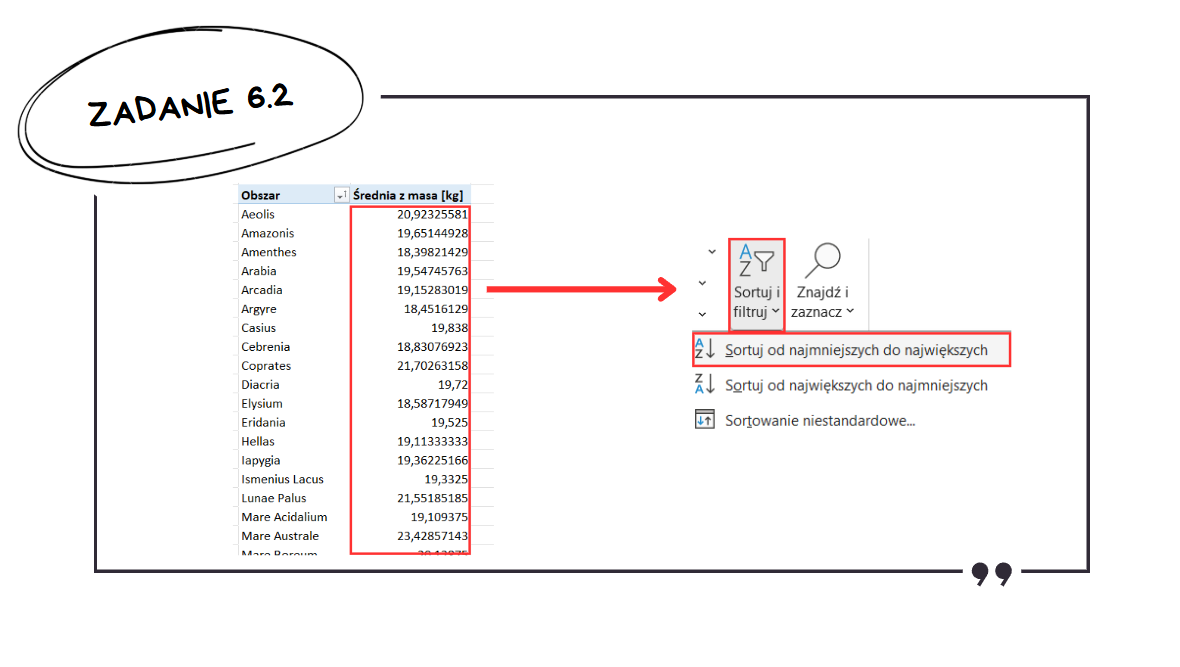

Zadanie 6.3: Okresy 7–dniowe – Maksymalna Masa

Aby ułatwić sobie rozwiązywanie, można dodać kolumnę określającą dzień danego okresu.
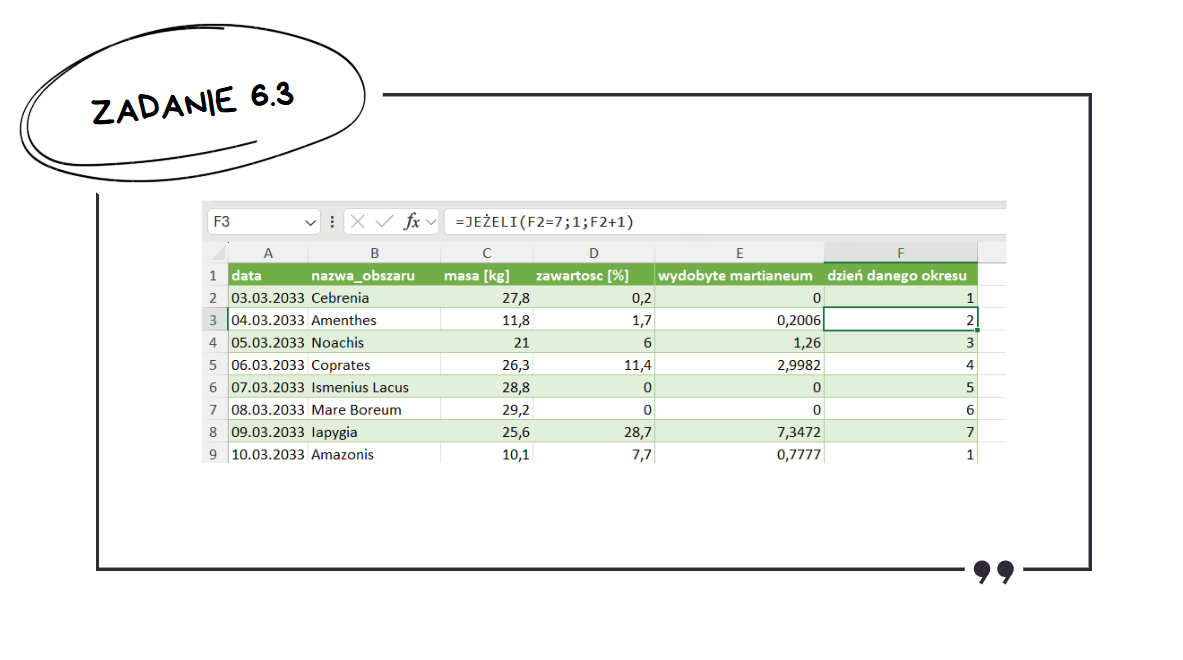
Następnie w kolejnej kolumnie piszemy formułę, która będzie obliczać dotychczasową sumę w danym okresie. Jeżeli dzień okresu jest różny od 1, to dodajemy do sumy z dnia poprzedniego masę przywiezioną z danego dnia. Jeżeli dzień jest równy 1, to resetujemy i ustawiamy wartość w kolumnie na masę przywiezioną danego dnia.
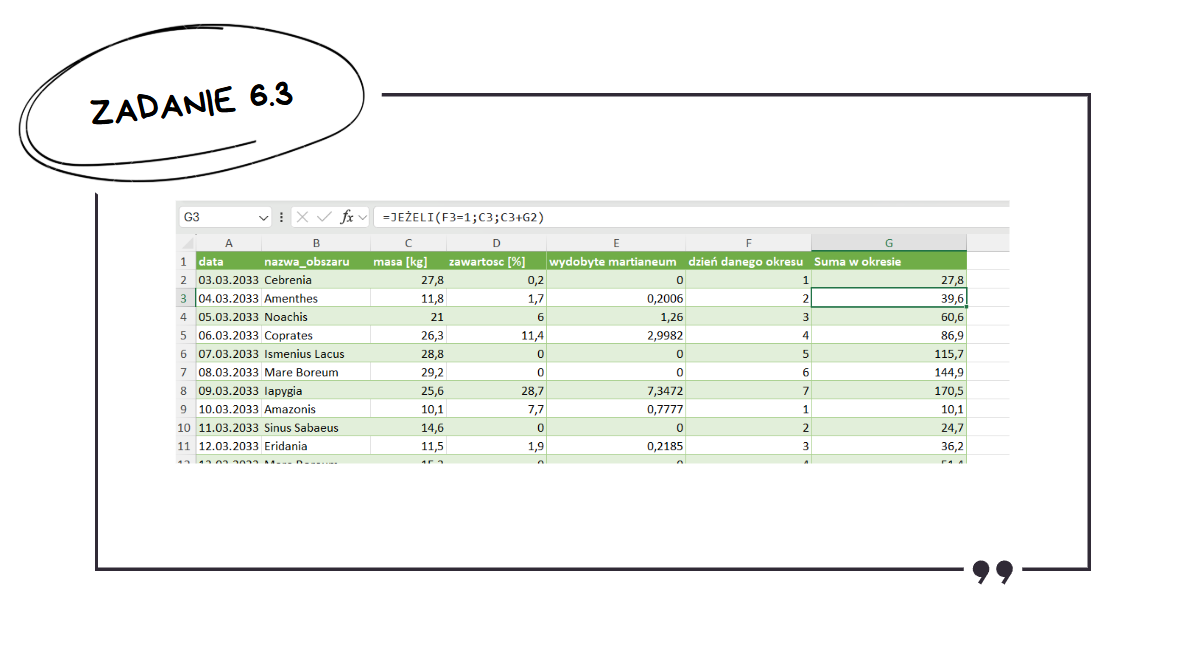
Teraz wystarczyło użyć funkcji MAX() do znalezienia największej masy.
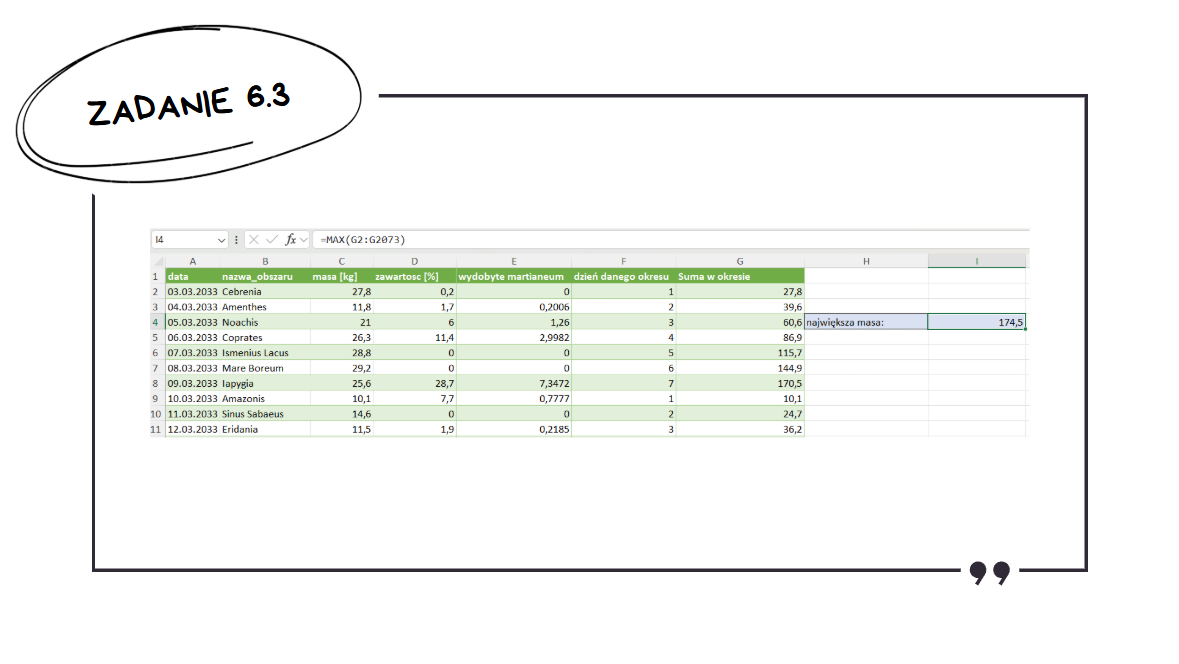
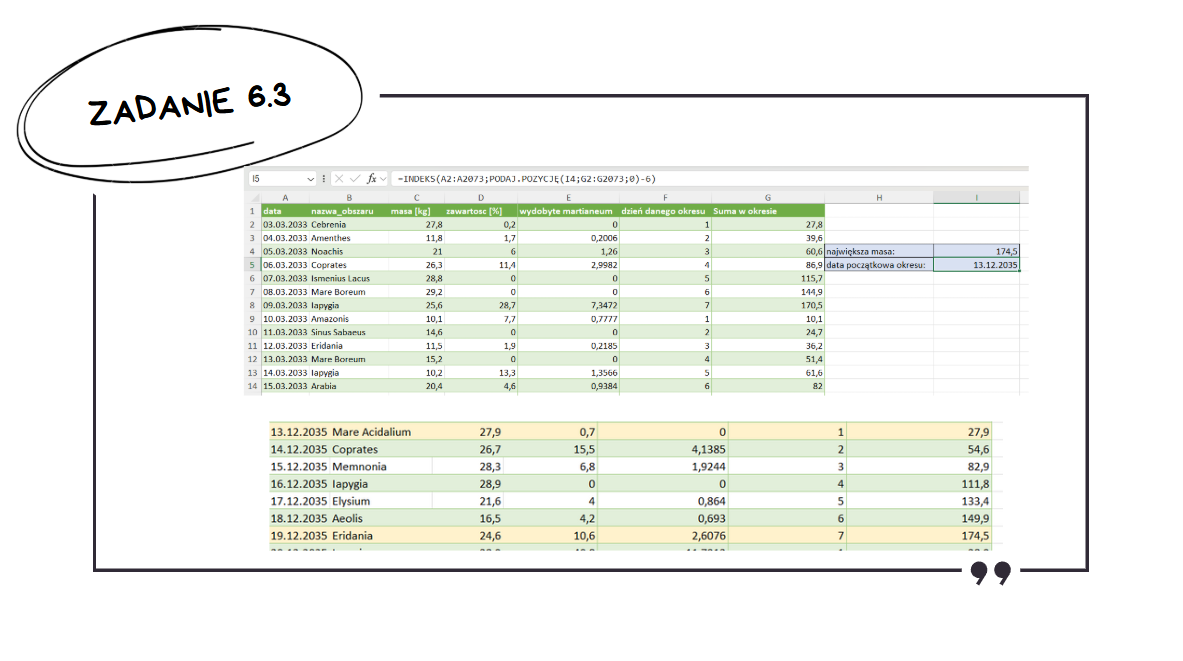
Znaleźć datę początkową możemy po prostu ręcznie – np. korzystając z formatowania warunkowego. Jednak zawsze w takich zadaniach proponuję zrobić to odpowiednią formułą – zmniejszamy wtedy prawdopodobieństwo, że coś źle odczytamy czy pominiemy.
Używamy formuły PODAJ.POZYCJĘ() do znalezienia, w którym wierszu tabeli występuje maksymalna masa. Przekazujemy ten znaleziony numer wiersza do funkcji INDEKS() – pomniejszony o 6, bo szukamy pierwszego dnia okresu. Tak napisana formuła zwróciła pierwszy dzień okresu, w którym osiągnięto maksymalną sumę.
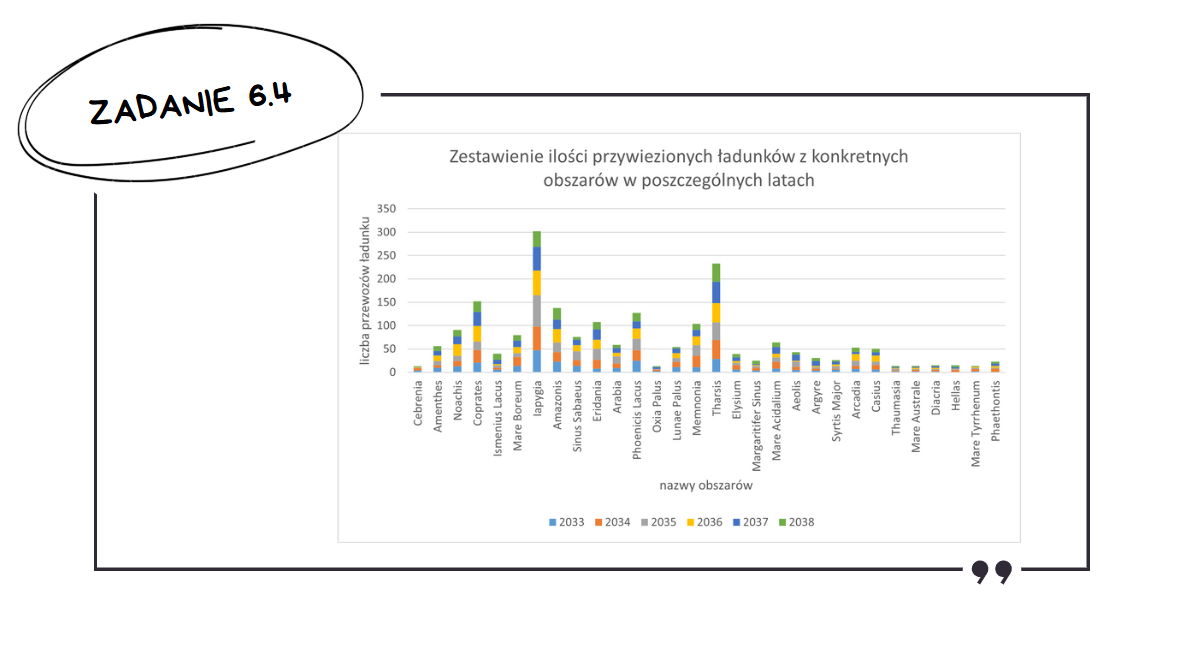
Zadanie 6.4: Wykres Skumulowany Kolumnowy

To zadanie również możemy zrobić za pomocą tabeli przestawnej, jednak wtedy stworzenie wykresu może być dość uciążliwe. W celu znalezienia unikalnych nazw obszarów można skorzystać z funkcji UNIKATOWE().
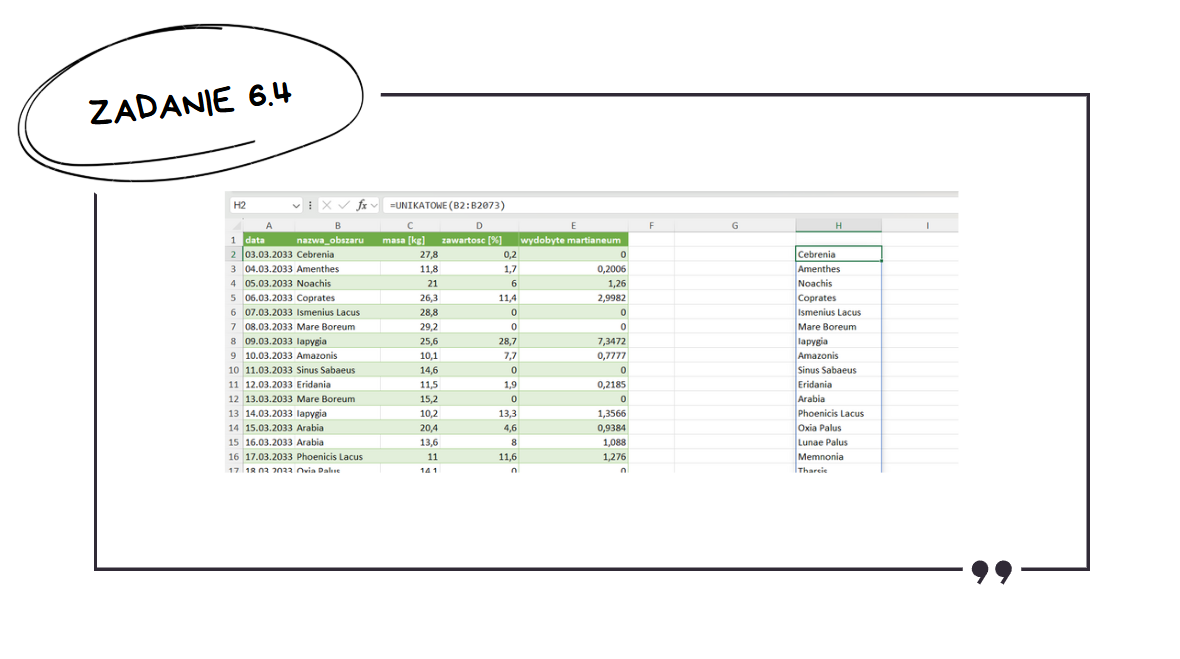
Do tabeli dodajemy pomocniczą kolumnę rok.
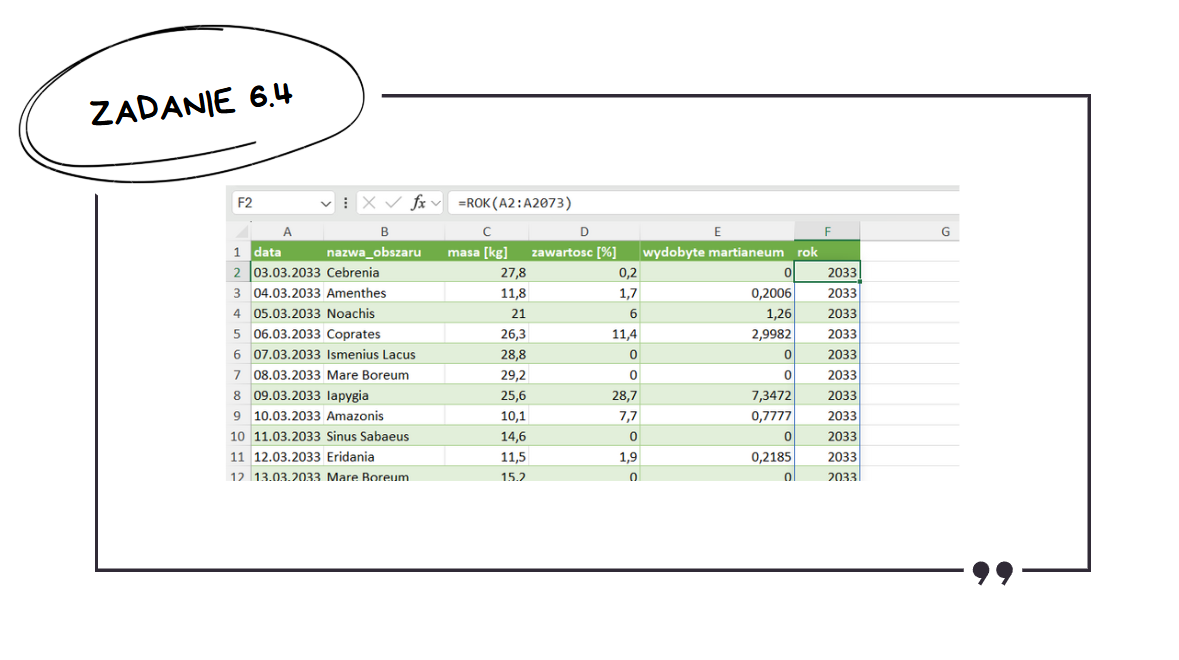
Tworzymy tabelę, w której kolejne wiersze to będą nazwy obszarów, a kolumny to lata 2033 – 2038. W tej tabeli za pomoca funkcji LICZ.WARUNKI() zliczamy liczbę wystąpień odpowiedniego obszaru w odpowiednim roku.
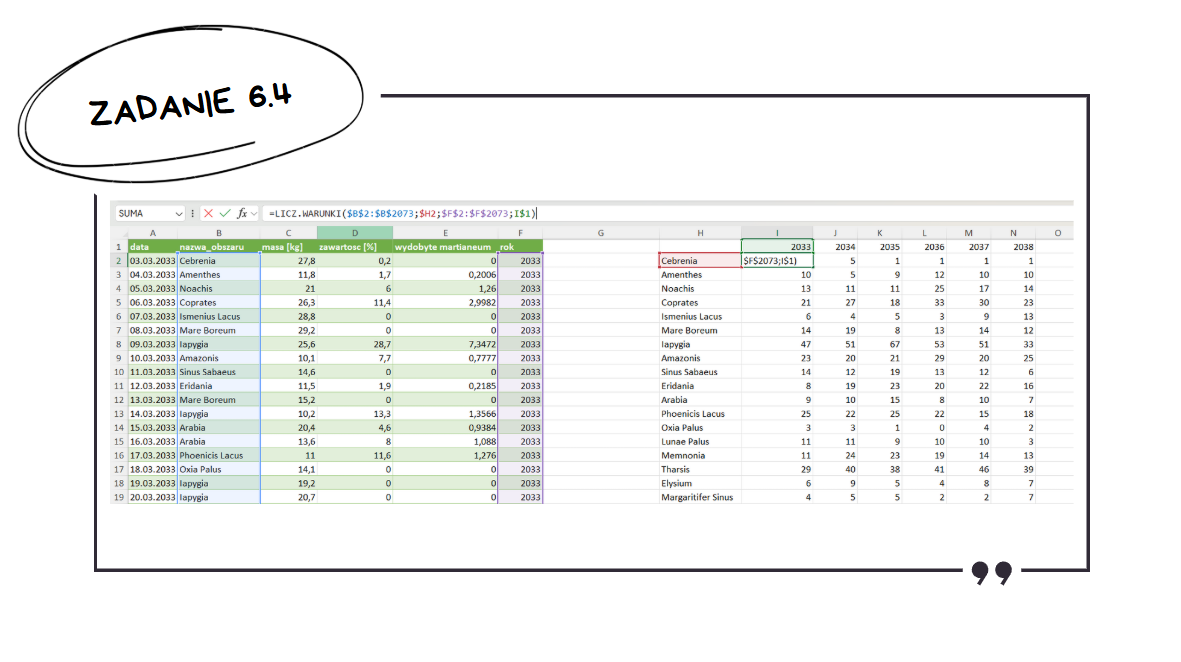
Samo tworzenie wykresu na maturze nie jest niczym nowym, jednak chyba po raz pierwszy CKE wymaga wykresu skumulowanego kolumnowego.
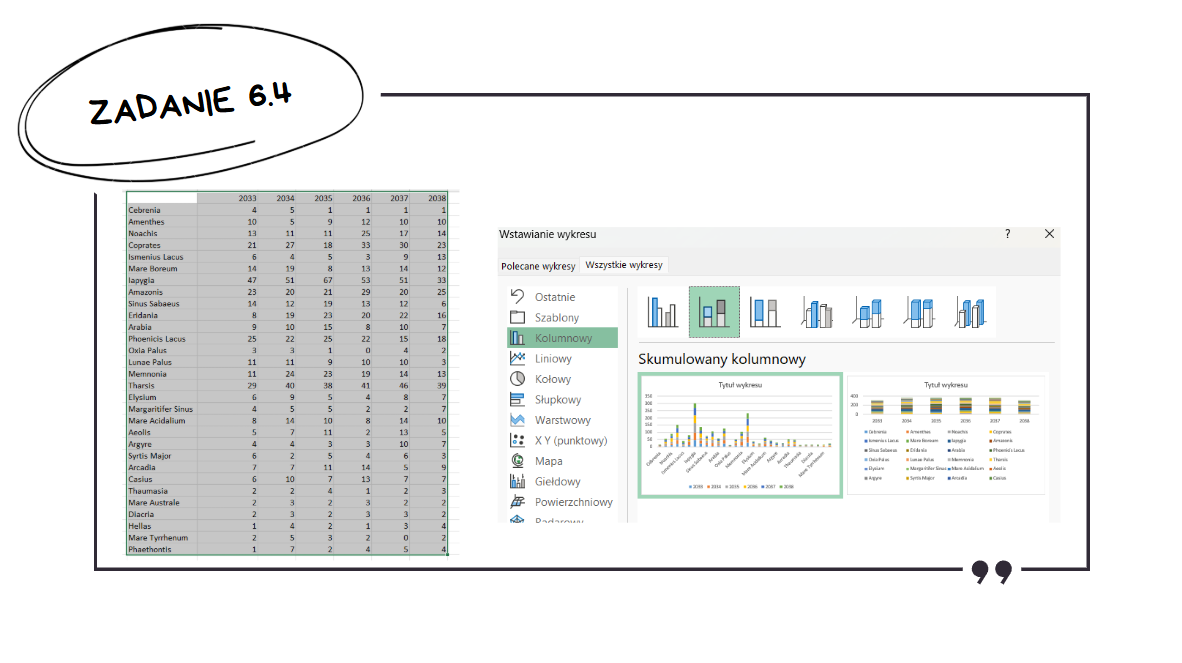
Finalnie należy opisać wykres zgodnie z poleceniem. Nadajemy tytuł wykresu, nazywamy osie, dodajemy legendę.
Zadanie 6.5: Symulacja Pracy Stacji

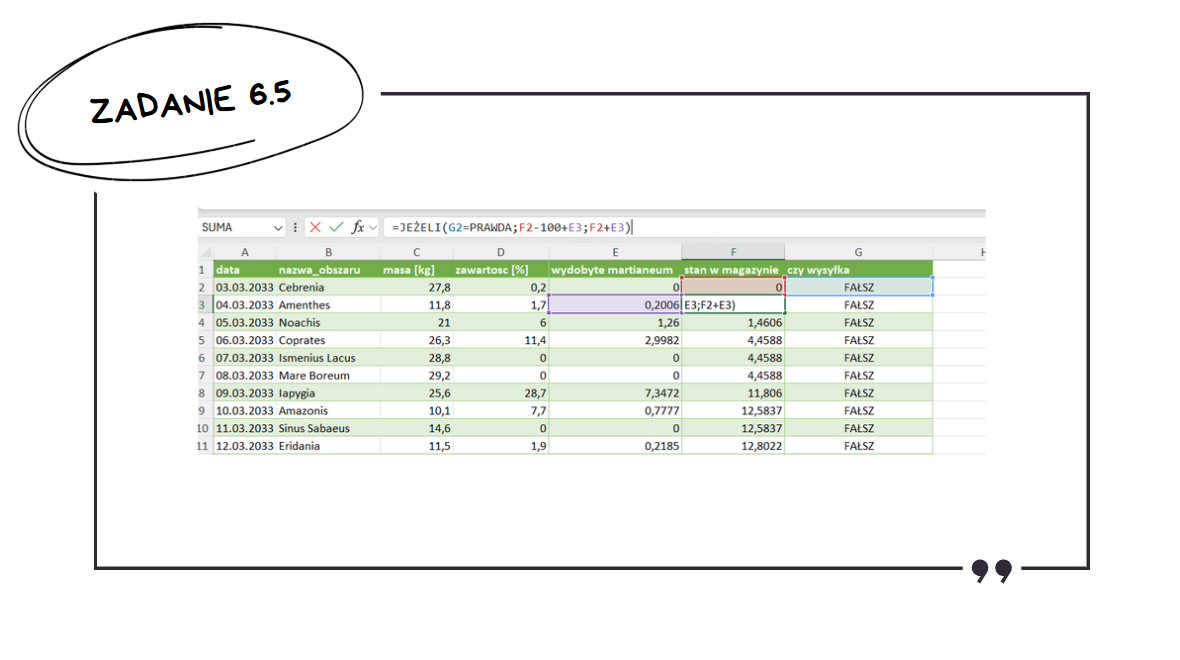
Zaczniemy od dodania dwóch nowych kolumn – stan w magazynie oraz czy wysyłka. Stan w magazynie, w przypadku gdy poprzedniego dnia nie było wysyłki, będzie równy stanowi z dnia poprzedniego powiększonemu o martianeum wydobyte danego dnia. W przypadku wysyłki od stanu dnia poprzedniego odejmiemy 100. Kolumna czy wysyłka będzie sprawdzać czy stan w magazynie jest większy lub równy 100.
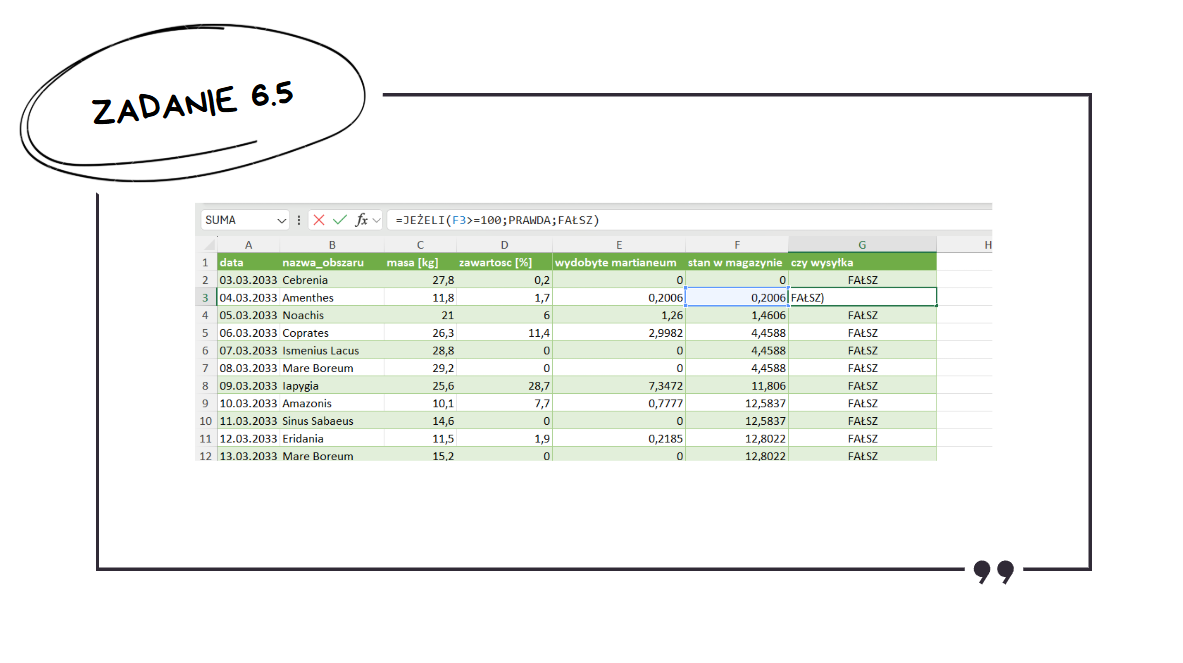
Teraz wystarczy zliczyć liczbę "PRAWDA" w kolumnie czy wysyłka.
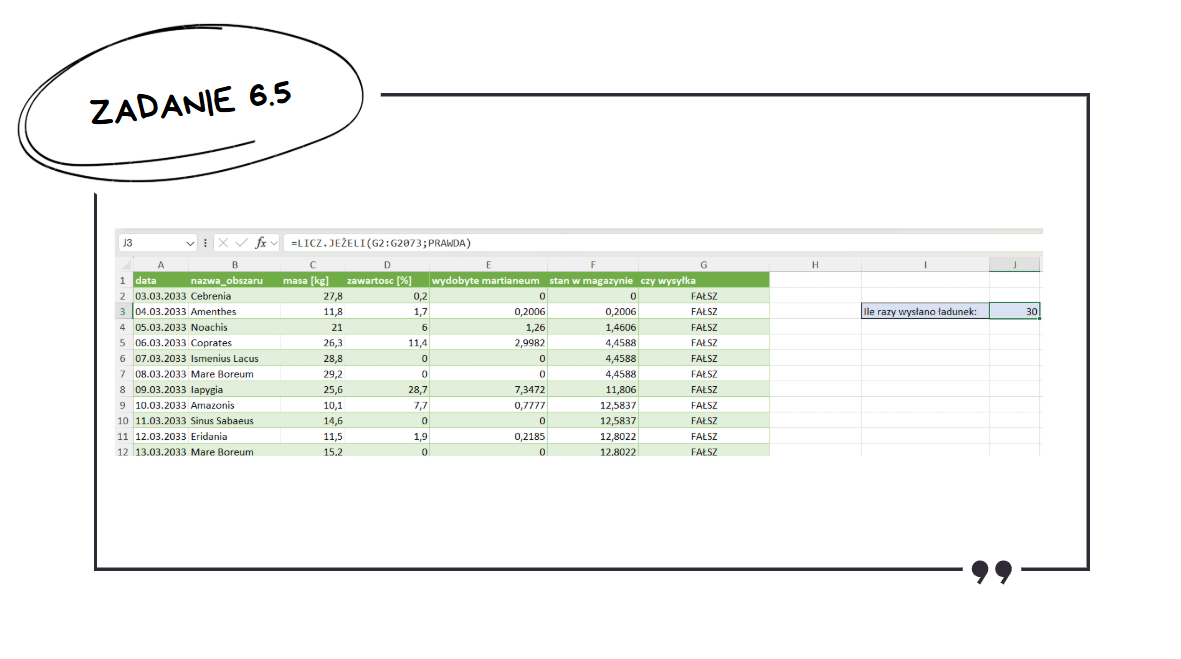
Pierwszą i ostatnią przesyłkę można by wyszukać ręcznie, ale tutaj też zrobimy to za pomocą Excela. W tym celu dodamy kolumnę, która będzie przechowywać liczbę wysłanych do danego momentu ładunków.
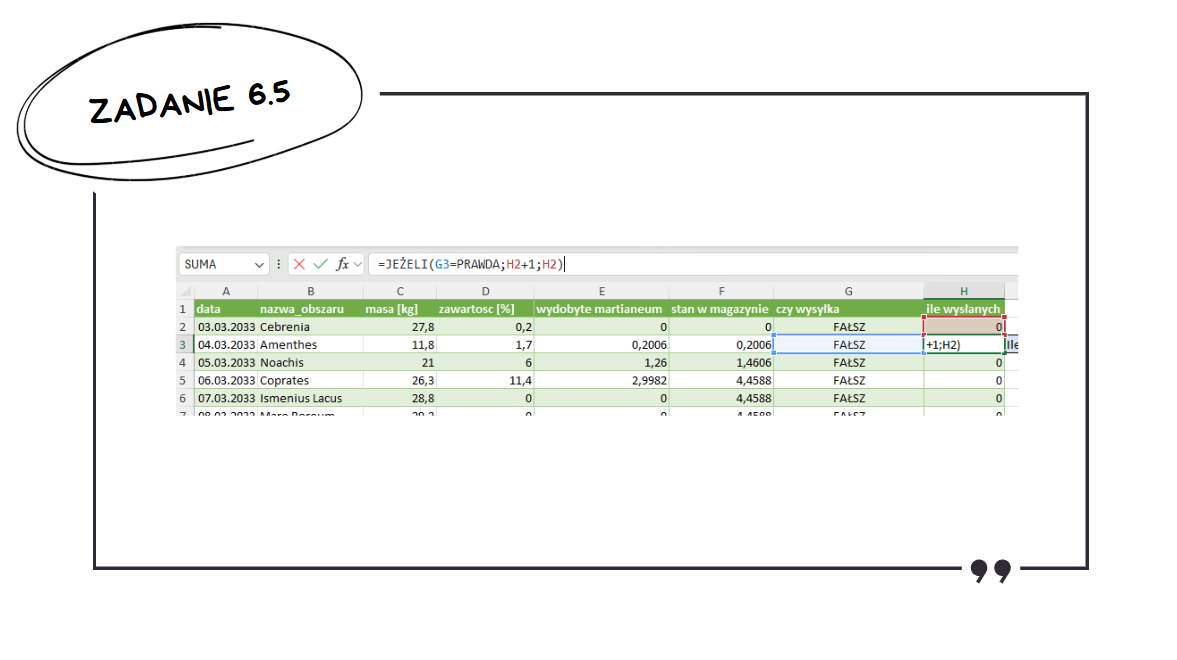
Funkcja PODAJ.POZYCJĘ() w Excelu zwraca indeks pierwszego wystąpienia wyszukiwanego elementu w tablicy. Wykorzystamy ten fakt do tego, aby wyszukać pierwsze wystąpienie jedynki w tablicy i następnie za pomocą funkcji INDEKS() wypiszemy datę mu odpowiadającą.
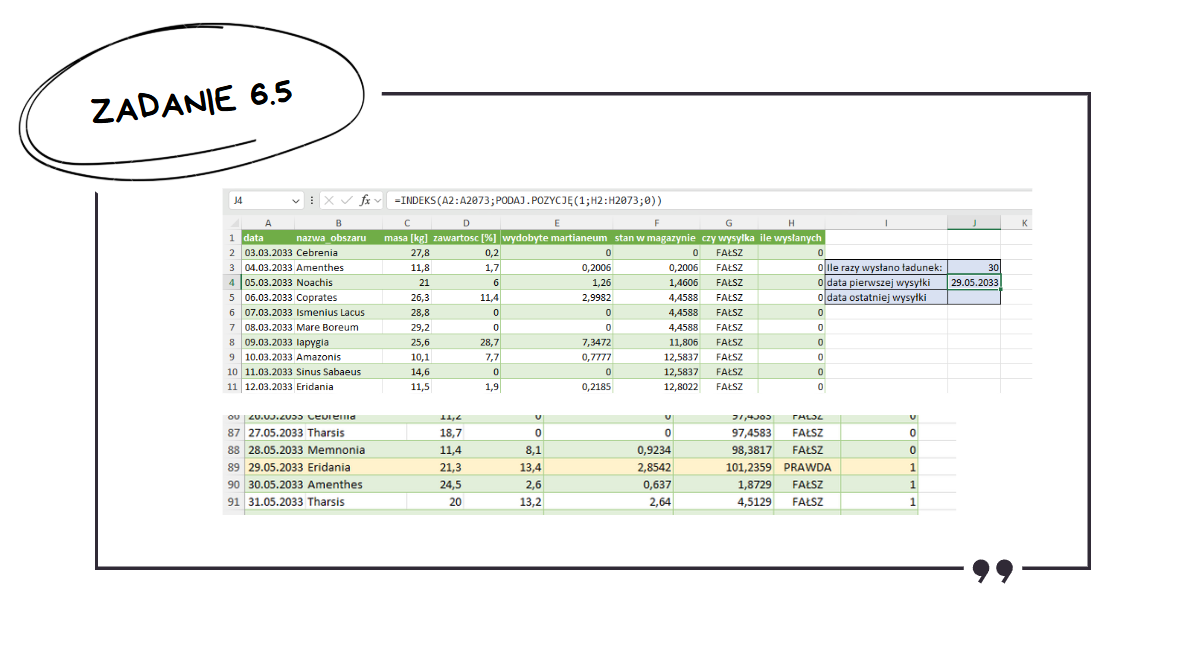
Wyszukiwanie ostatniej przesyłki robimy analogicznie – jedyną różnicą jest to, że szukamy 30 a nie jedynki.
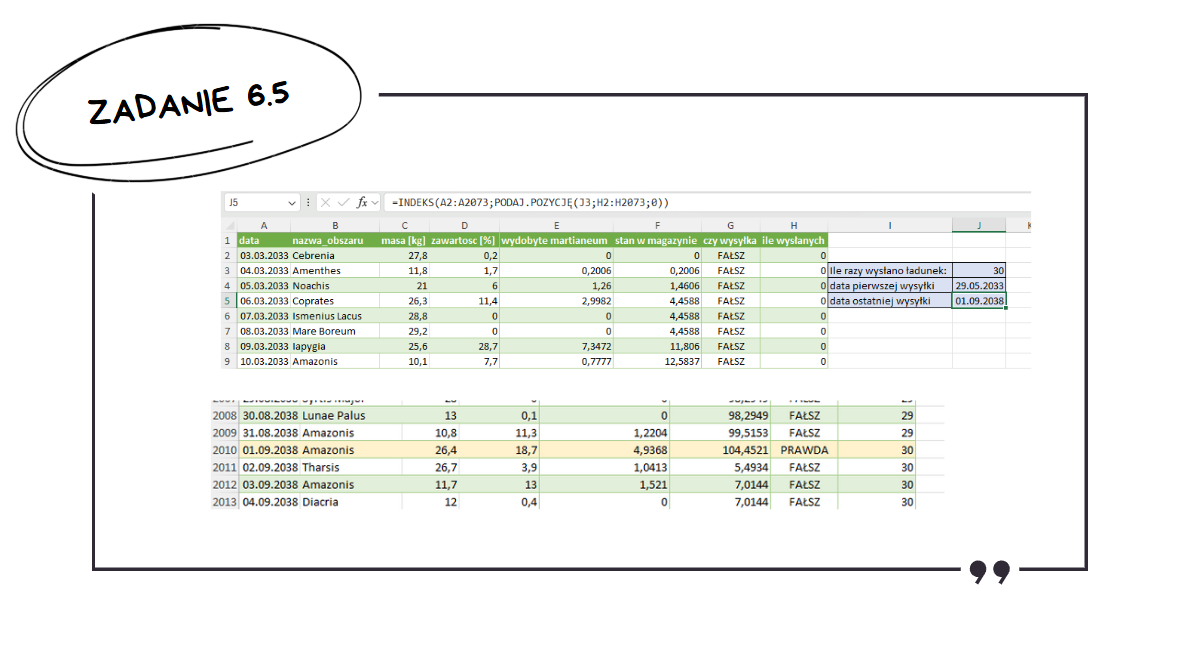
Podobnie jak w przypadku zadań z programowania, wyniki należy zapisać w pliku o takiej nazwie, jak określono w poleceniu. Na uwagę zasługuje jedynie to, że pełną odpowiedź do zadania 6.4. stanowi zarówno wykres, jak i zestawienie w pliku .txt.

Zadanie oceniam jako średnie pod kątem poziomu trudności. Jeśli miałeś/miałaś jakąś styczność z arkuszami kalkulacyjnymi wcześniej – a to zadanie wydaje Ci się bardzo trudne – nic dziwnego, bo trzeba zacząć, step by step, od łatwych matur, po średnie, trudne i najtrudniejsze. Wtedy takie zadanie jak to staje się przyjemnością podczas matury, w porównaniu do tych najtrudniejszych. Wszystko to kwestia ćwiczenia, odpowiednich zadań i czasu, żeby to wszystko przerobić. Im wcześniej zaczniesz, tym lepiej.
Zadanie 7: Poszukiwanie Wody na Marsie – Matura z Informatyki 2025

Zadanie 7. to klasyczne zadanie z baz danych realizowane w Microsoft Access. Dotyczyło analizy danych z misji łazików marsjańskich poszukujących wody. Przed rozwiązaniem tego zadania należy zaimportować pliki .txt:
- laziki.txt – dane o łazikach marsjańskich.
- obszary.txt – informacje o obszarach badań.
- pomiary.txt – wyniki pomiarów.
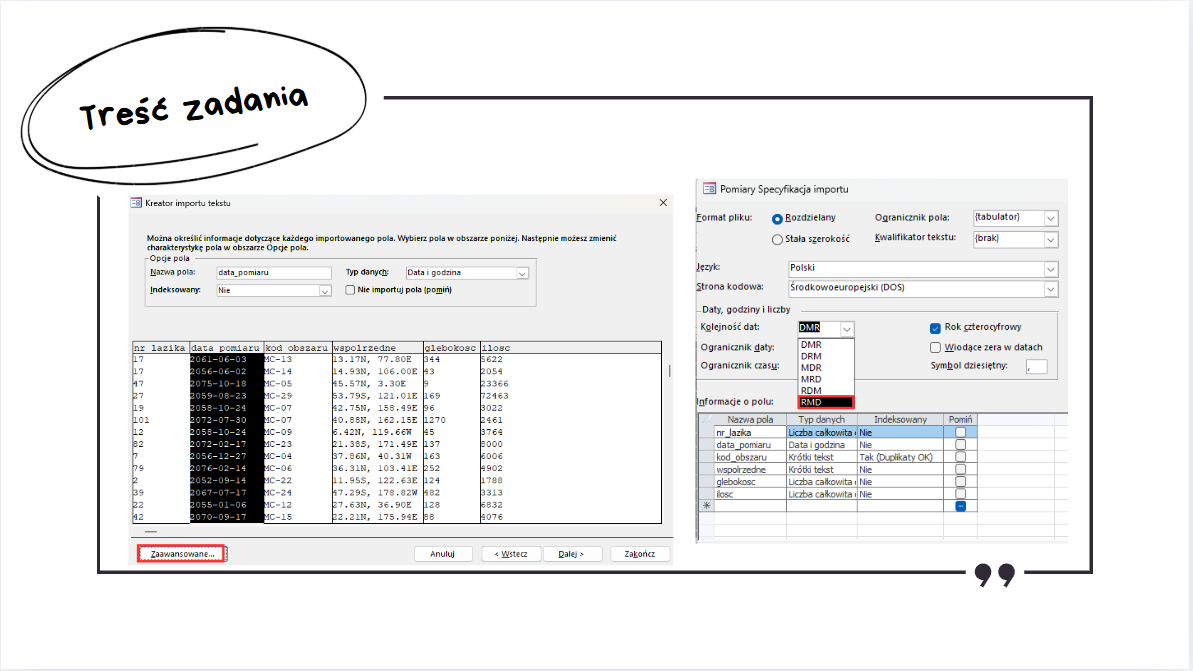
Po poprawnym zaimportowaniu tych trzech plików należy pamiętać o ustawieniu odpowiednich relacji między tabelami.
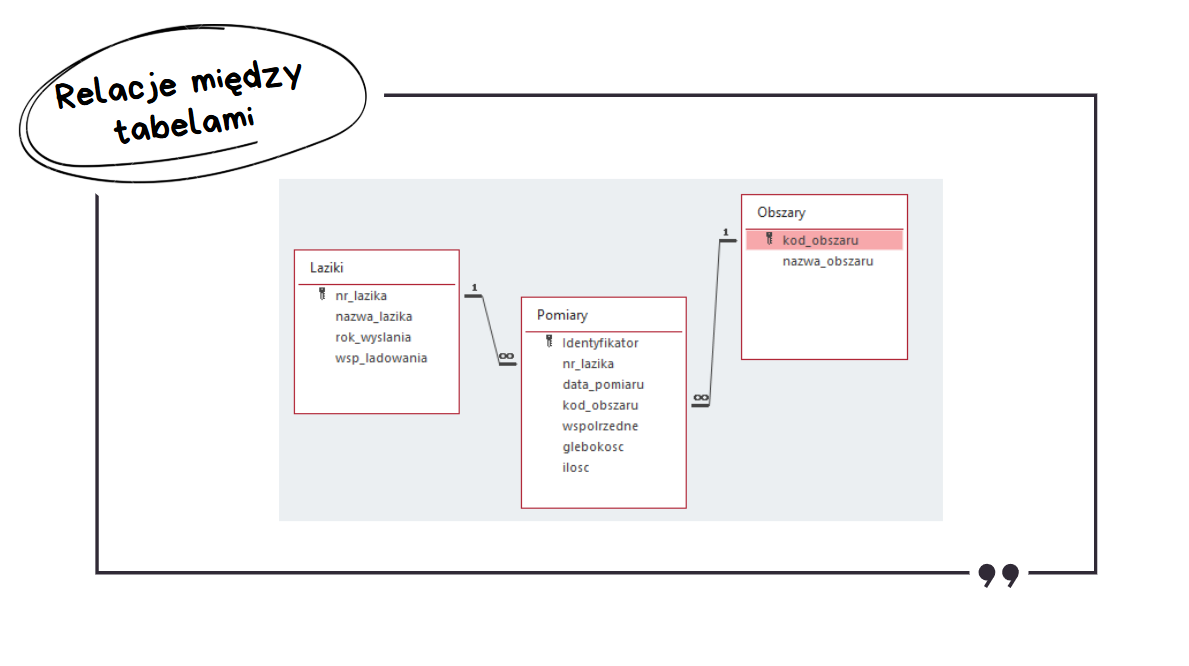
Zadanie 7.1: Suma Ilości Wody wg Obszarów

Aby rozwiązać to zadanie, wystarczy stworzyć jedną kwerendę – pogrupować po nazwie obszaru i zsumować łączną liczbę m3 wody dla każdego z nich. Dodatkowo konieczny będzie warunek, że głębokość ma być mniejsza lub równa 100.
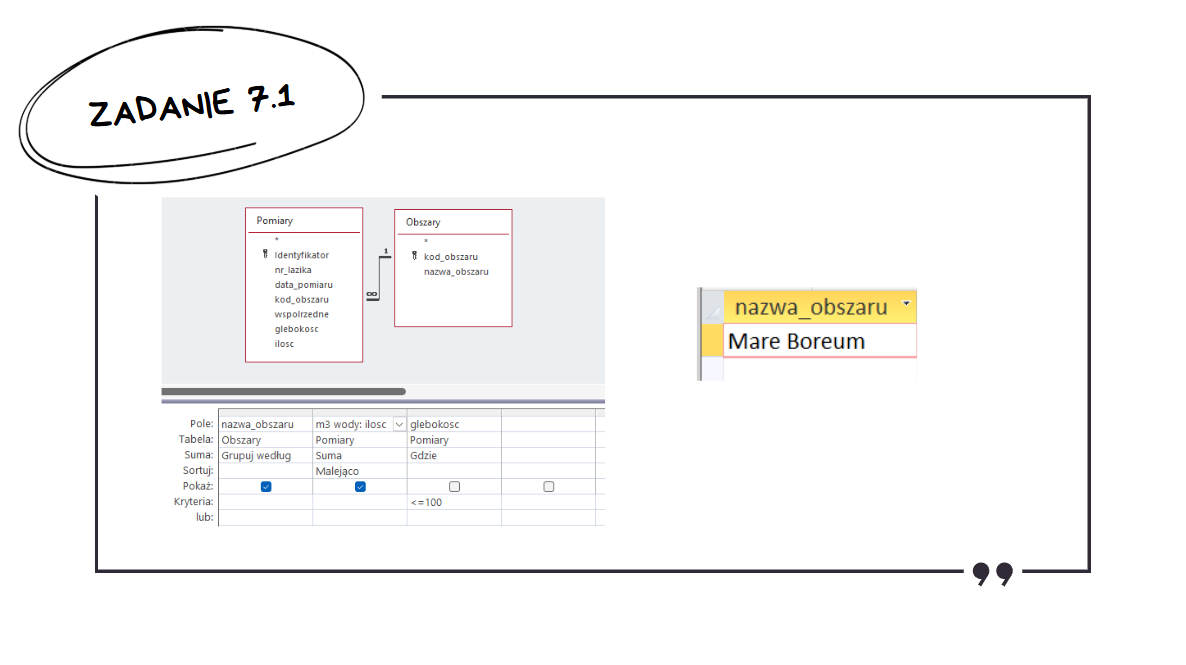
Bardzo proste zadanie – funkcje agregujące to podstawa Accessa.
Zadanie 7.2: Najdłużej Pracujący Łazik

W tym zadaniu, już trzeba będzie skorzystać z dwóch kwerend. Pierwsza pomocnicza powinna wyszukać dla każdego łazika datę pierwszego i ostatniego pomiaru korzystając z funkcji maksimum i minimum.
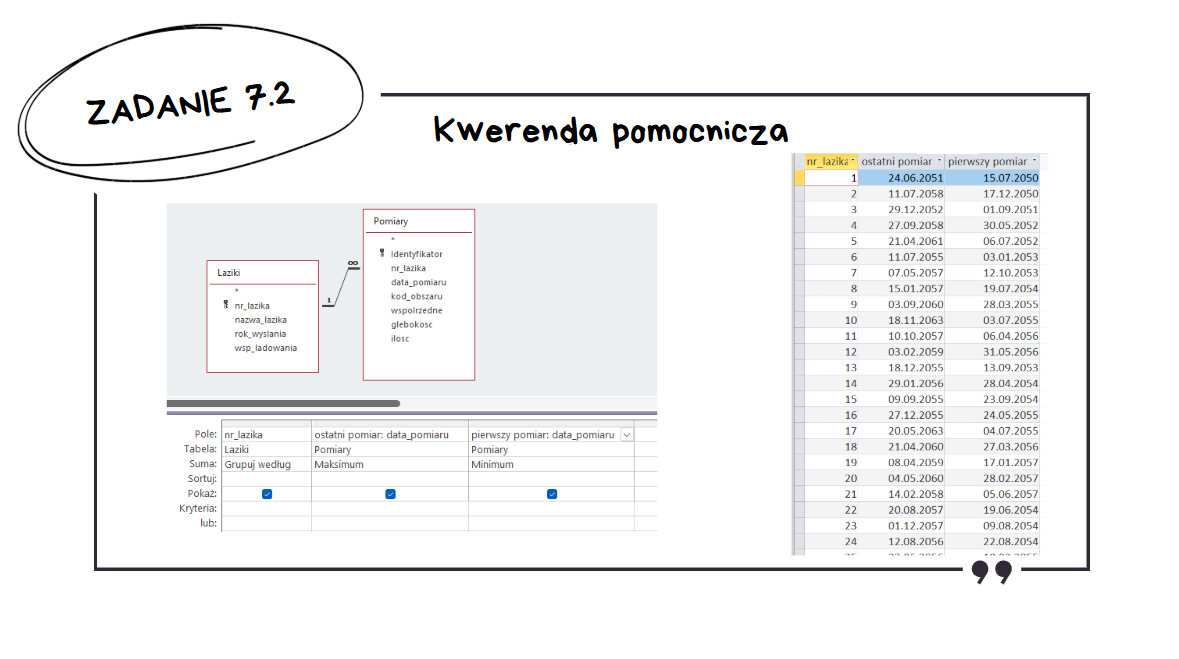
W kolejnej kwerendzie sortujemy malejąco po różnicy między najpóźniejszą oraz najwcześniejszą datą. Należy pamiętać o limitowaniu wyników do jednego wiersza.
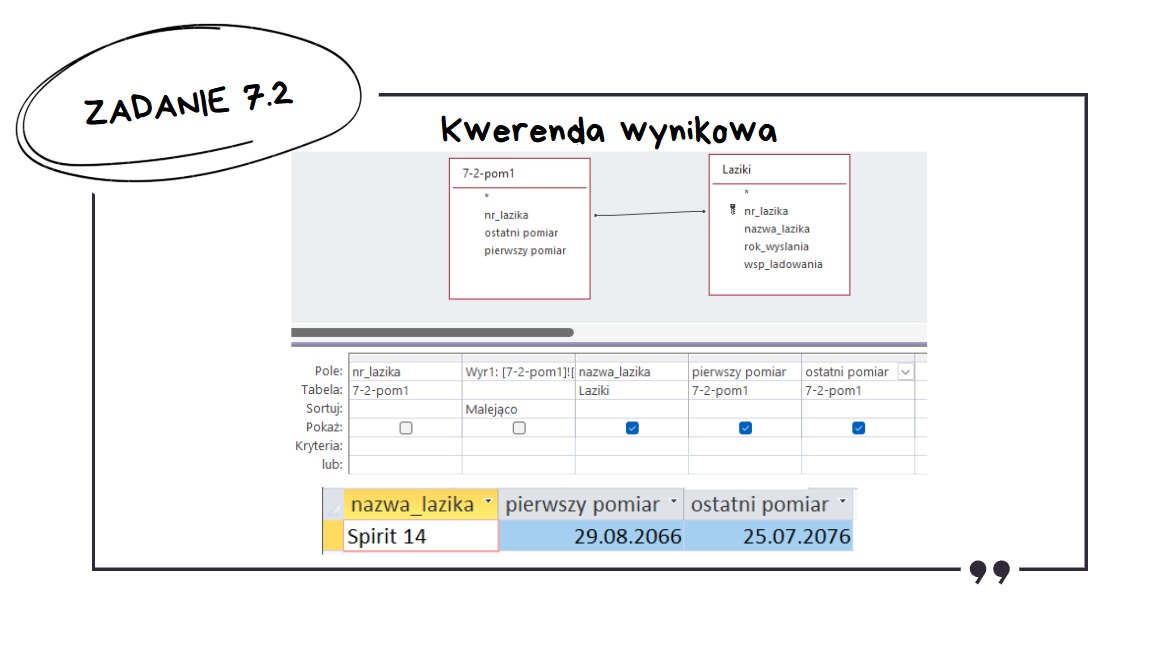
Zadanie 7.3: Kwerenda Wyszukująca Niepasujące Dane

To zadanie jest typowym zadaniem wymagającym użycia kwerendy wyszukującej niepasujące dane – ten typ pojawia się na praktycznie każdej maturze. Do takich zadań trzeba podejść trochę "na odwrót". W kwerendzie pomocniczej wypiszemy obszary, na których jakiś łazik wykonał przynajmniej jeden pomiar w tym samym roku w którym został wysłany z Ziemi.
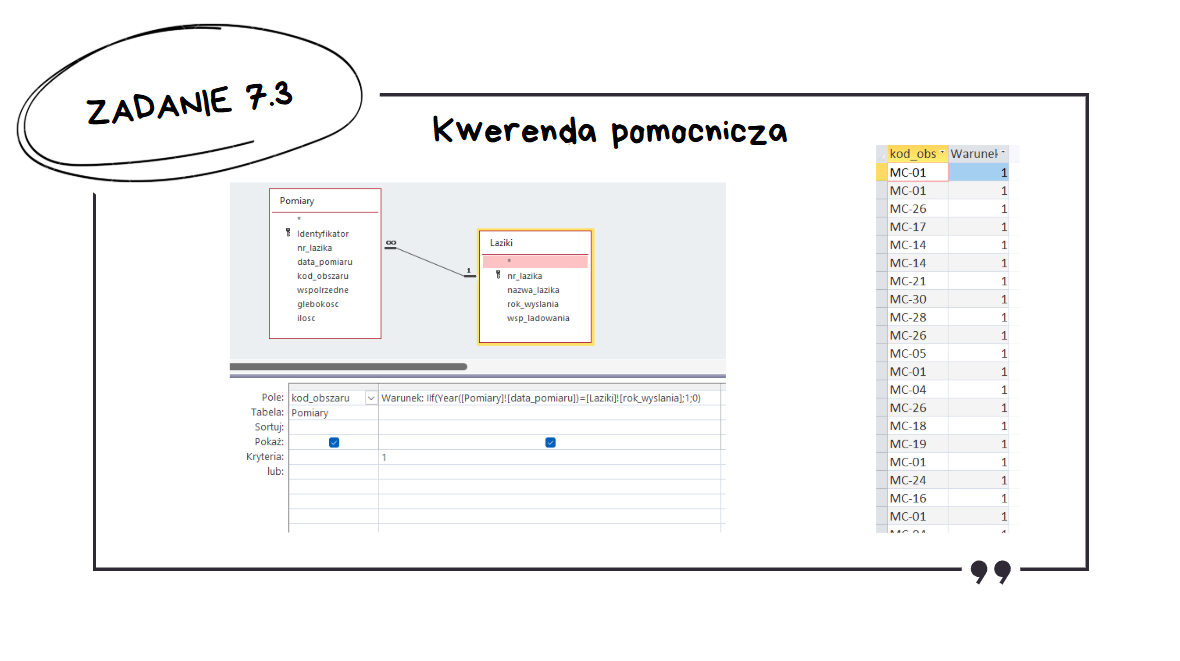
Jak utworzyć kwerendę wyszukującą niepasujące dane?
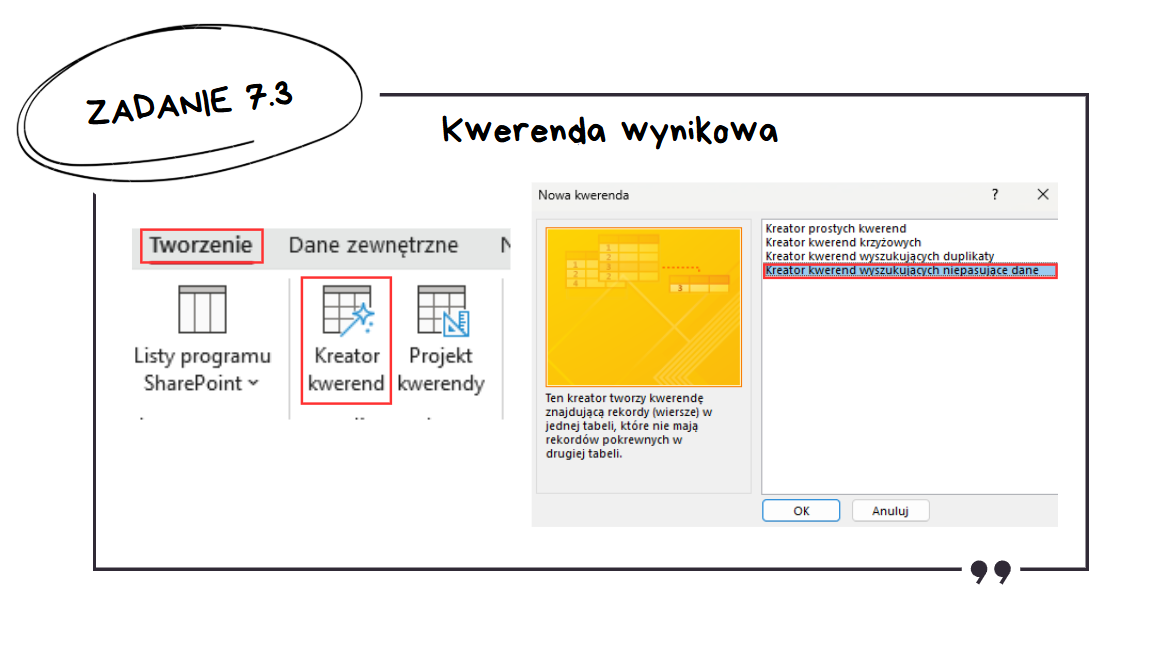
Będziemy chcieli znaleźć obszary, które występują w tabeli z obszarami, ale nie występują w kwerendzie, którą przed chwilą utworzyliśmy. Dlatego, tabelą która zawiera rekordy, które mają występować w wyniku kwerendy, jest tabela Obszary, a kwerendą, która zawiera pokrewne rekordy, będzie pomocnicza kwerenda.
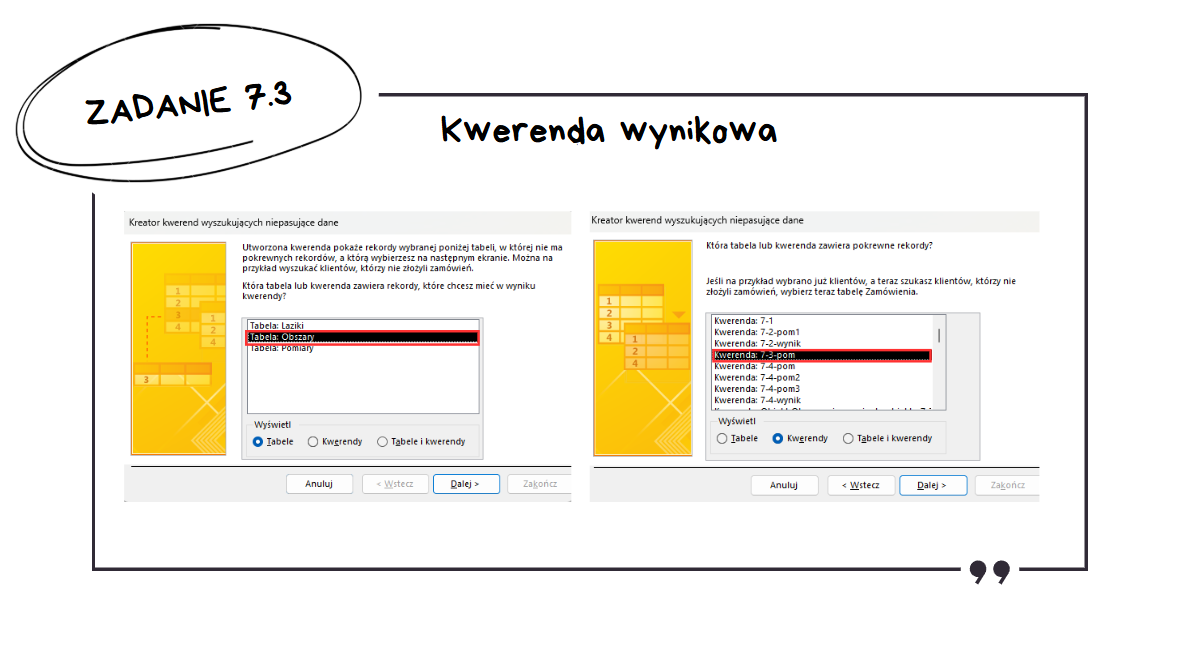
W obu tych tabelach występuje pole kod_obszaru, oraz w wyniku kwerendy chcemy zobaczyć nazwę obszaru.
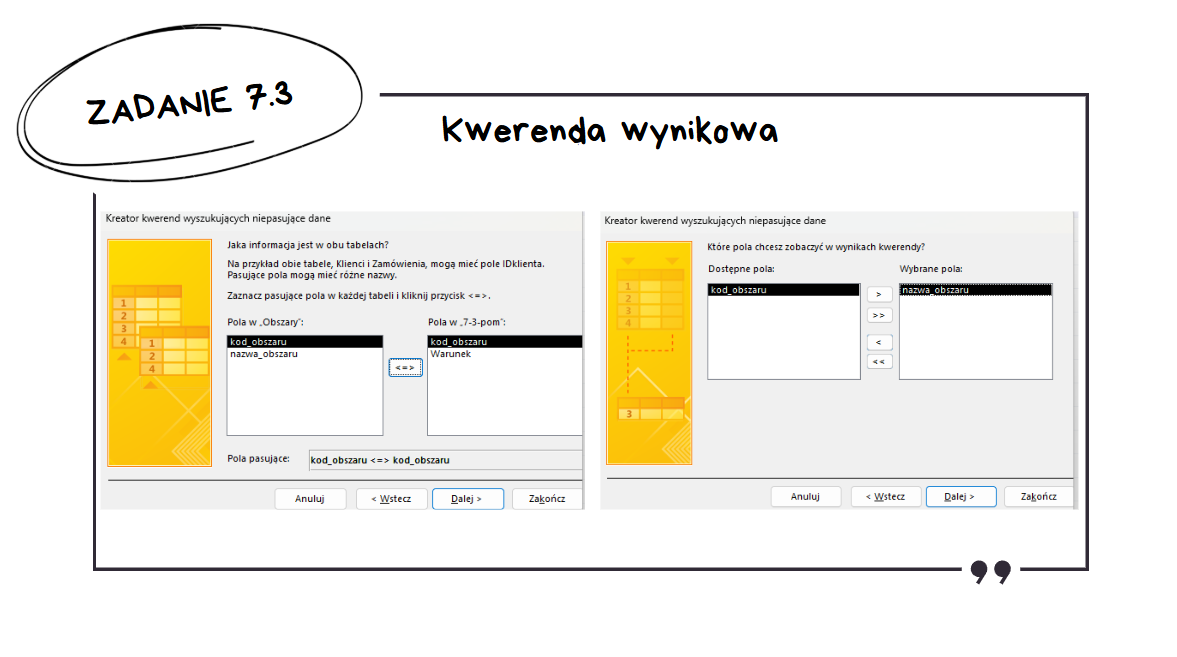

Zadanie 7.4: Analiza Półkul

W tym zadaniu także będzie trzeba skorzystać z kilku kwerend pomocniczych. W pierwszej kwerendzie wypisujemy te łaziki, które wylądowały na półkuli południowej – korzystamy z LIKE do znalezienia współrzędnych lądowania, które gdziekolwiek zawierają S.
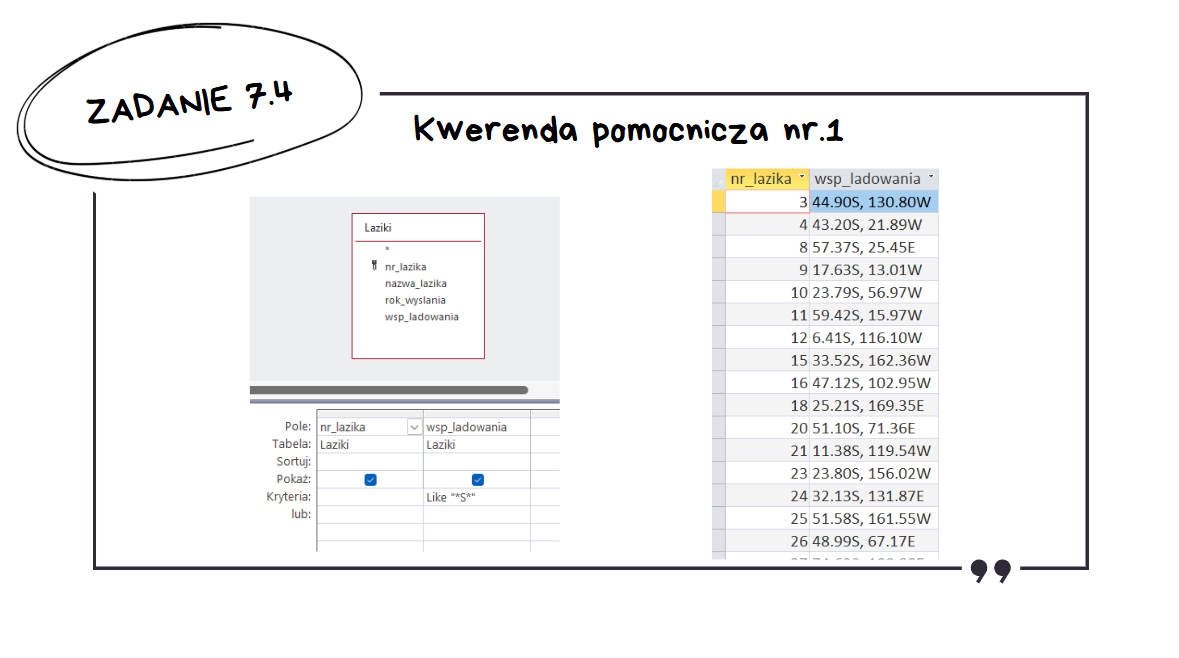
W następnej kwerendzie piszemy IIF–a, w którym jeżeli współrzędne pomiarów są na północnej półkuli, to piszemy N, a jeżeli na południowej, to piszemy S.

W następnej kwerendzie zliczamy dla każdego łazika z poprzedniej kwerendy ile półkul odwiedził.

W wynikowej kwerendzie łączymy kwerendy nr. 1 i nr. 3 relację (po numerze łazika). Wypisujemy nazwy łazików, które odwiedziły obie półkule.
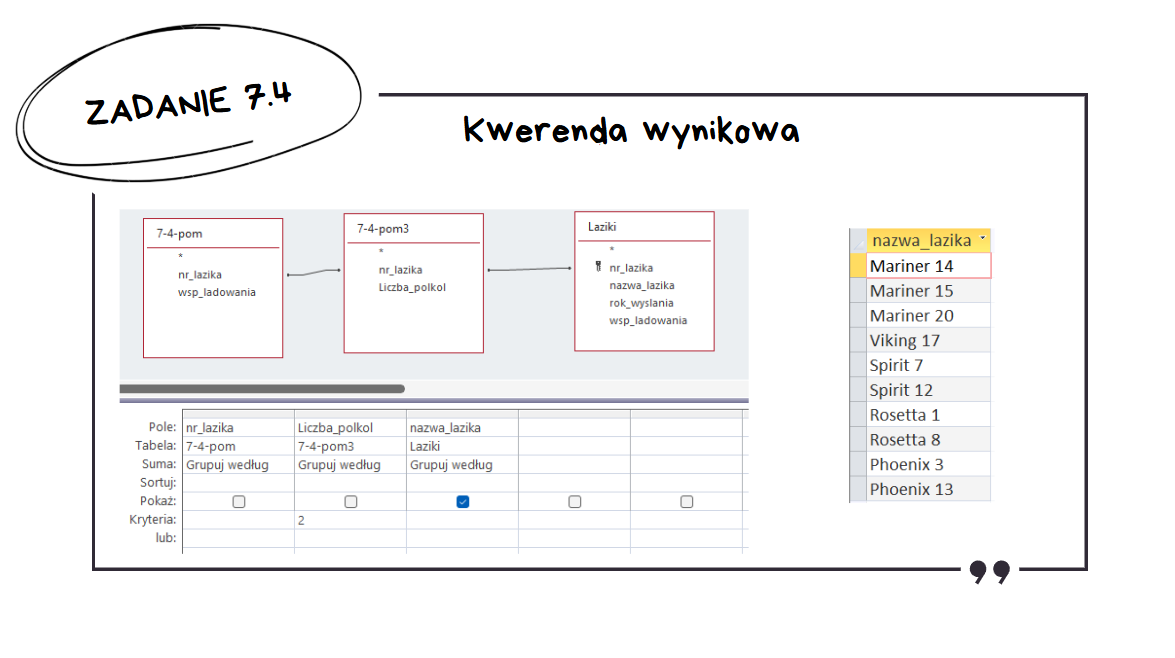
Ten podpunkt był chyba najtrudniejszy z całego zadania. Tego typu podpunkty, wymagające stworzenia kilku kwerend pomocniczych i połączenia ich relacją, zdarzają się często na maturach z nowej formuły, więc nie można tutaj mówić o zaskoczeniu.
Zadanie 7.5: Zapytanie SQL

SELECT DISTINCT p.nazwa FROM Producent p
INNER JOIN Laziki l ON p.kod_producenta = l.kod_producenta
INNER JOIN Pomiary pm ON l.nr_lazika = pm.nr_lazika
INNER JOIN Obszary o ON pm.kod_obszaru = o.kod_obszaru
WHERE o.nazwa_obszaru = 'Arcadia' AND YEAR(pm.data_pomiaru) = 2060;Kluczowe elementy zapytania:
- Cztery tabele wymagające trzech JOIN–ów
- DISTINCT dla uniknięcia duplikatów
- Funkcja YEAR() do wydobycia roku z daty
- WHERE filtrujące obszar i rok
Nowości na maturze z informatyki 2025
- Tylko jedno zadanie algorytmiczne (zamiast standardowych dwóch).
- Pisemne dodawanie binarne – nowa forma zadania z systemów liczbowych.
- Wykres skumulowany kolumnowy – pierwszy raz wymagany przez CKE.
- Szczegółowe wymagania opisu wykresów – konkretne wskazówki dotyczące tytułów i legendy – jest to zmiana jak najbardziej na plus.
Jakie były kluczowe umiejętności potrzebne na maturę z informatyki 2025?
- Rekurencja i iteracja
- Systemy liczbowe
- Operacje na napisach
- Podstawowe algorytmy (NWD, sprawdzanie czy ciąg znaków jest palindromem)
- Kluczowe definicje teoretyczne
- Excel: funkcje agregujące, tabele przestawne, wykresy, przeprowadzanie symulacji
- Access: funkcje agregujące, kwerendy wyszukujące niepasujące dane
- SQL: łączenie tabel, funkcje dat
Jakie wnioski po maturze z informatyki 2025?
Matura była bardzo podobna do matur z poprzednich lat. Pierwsze 5 zadań, było relatywnie proste. Natomiast zadania z arkuszy kalkulacyjnych i baz danych były trochę bardziej wymagające – ale nie wykraczały znacząco poza typowy poziom matury. Uczniowie, którzy solidnie się przygotowali i przerobili wcześniejsze arkusze, powinni poradzić sobie bez problemu.

